- Identify the first significant figure (4).
- What is the place value of this figure (thousands).
- So we are rounding to the nearest thousand.
- Is 4,271 closer to 4,000 or 5,000? (we used number lines to visualise this, though most could do it easily without by this point as they were secure with rounding to thousands)
- Identify the first significant figure (4).
- What is the place value of this figure (hundreds).
- So we are rounding to the nearest hundred.
- Is 427 closer to 400 or 500?
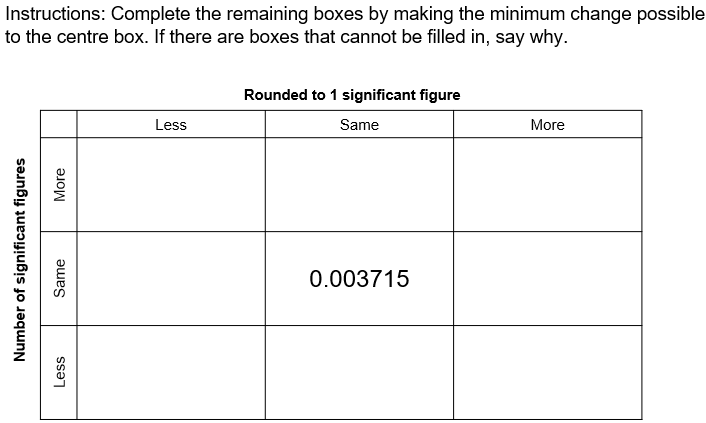
- Identify the first significant figure (4).
- What is the place value of this figure (hundredths).
- So we are rounding to the nearest hundredth.
- Is 0.0427 closer to 0.04 or 0.05?







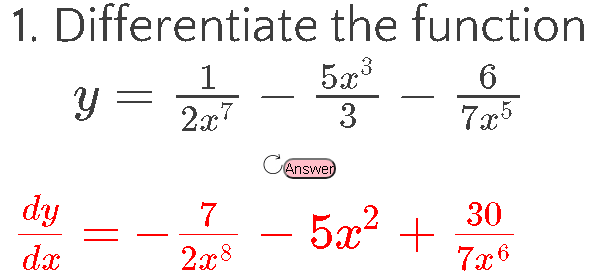
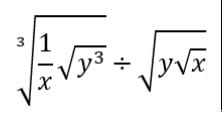
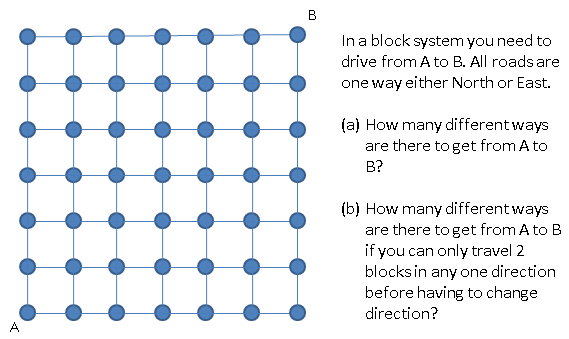
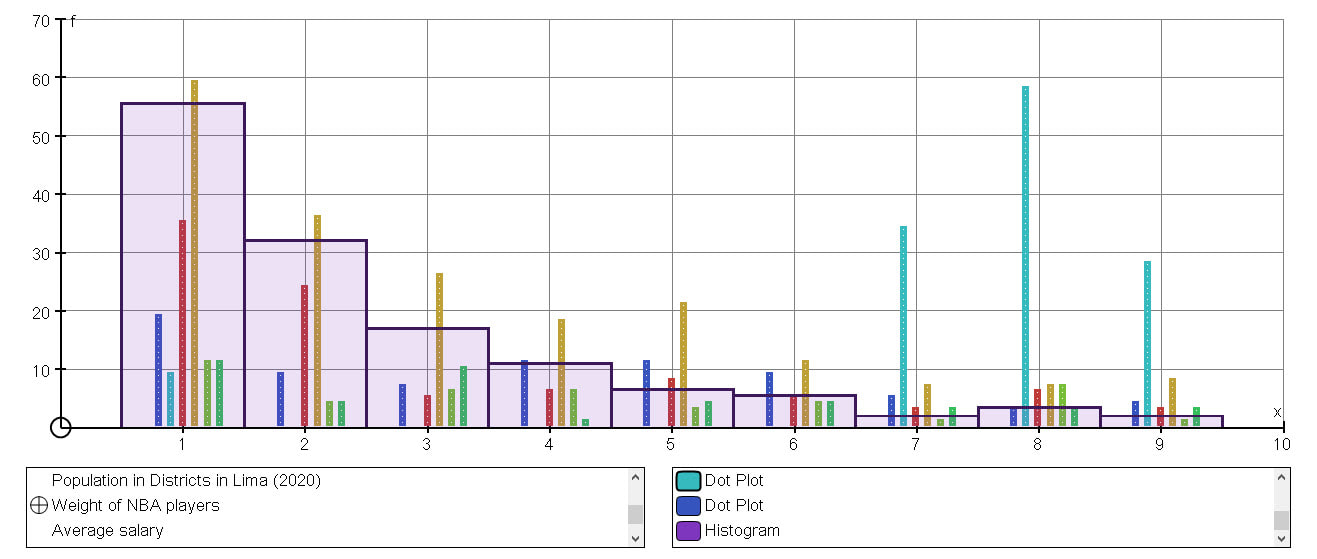


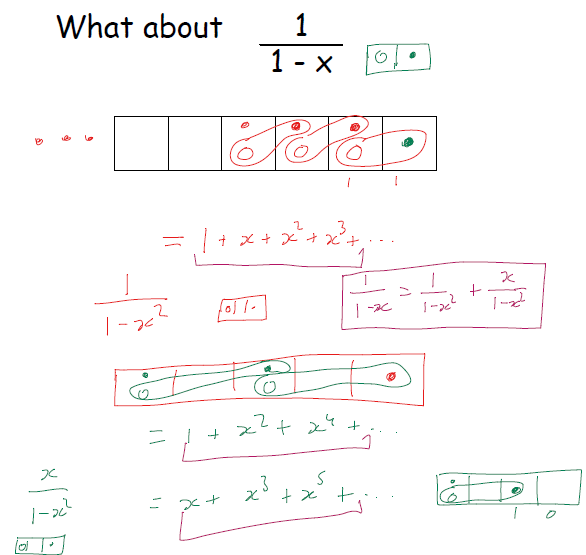


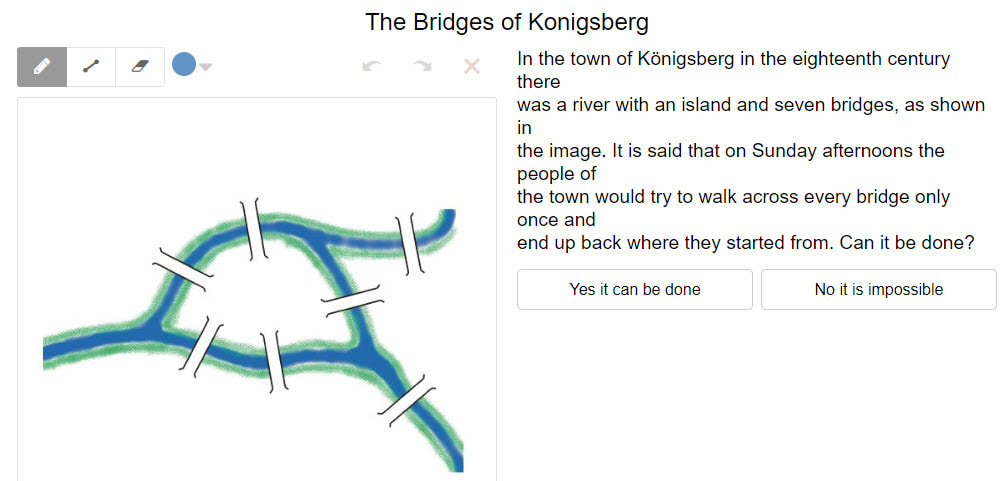
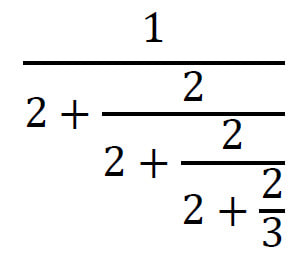
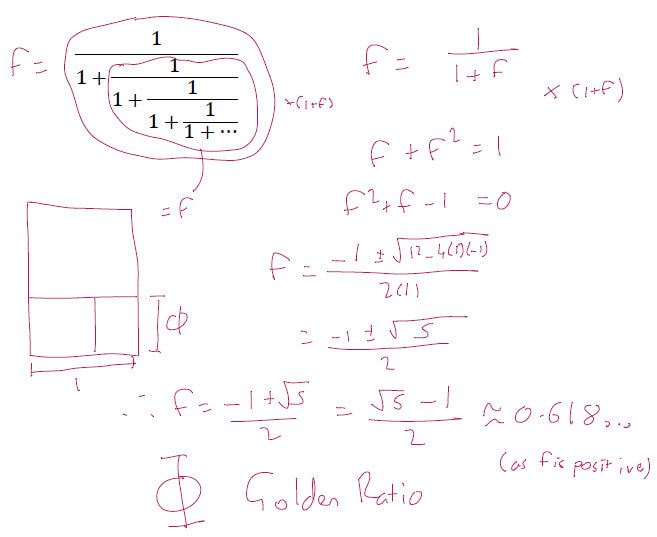










 RSS Feed
RSS Feed
