I have just finished reading The Teaching Delusion by Bruce Robertson, and it hit all the right notes for me. I found myself nodding along, lapping up what Robertson says, constantly thinking "This is exactly what I think, but said so much more eloquently." In fact, I am thinking of copying a few extracts to give to people when I can't put into words my own thoughts!
I jest, of course. There were plenty of insights in the book that I had not thought about before, and a couple of things I disagreed with.
The main premise is that no matter how good teaching is, it can always be better. This has been a point I have made at the start of each new school year since getting the job of T&L Coordinator, and my most recent phrasing has been "It is both our right and our duty to continue to improve our teaching". I use this wording carefully, to instil the idea that it is our right to want to continue to improve ourselves, get better at our jobs, and become better teachers. This aligns with Robertson's idea of a Professional Learning Culture. On the other hand, we serve a community of children and their parents (who, in my case, pay a fair amount of money for our services), and it is also our duty to them to do the best job we can, which includes continually improving our teaching. Our duty to the parents who pay, yes, but mainly our duty to the young people we have the pleasure of working with, whose future depends so much on what we say and do, how we make them feel, and what they learn from us.
Robertson asserts that The Teaching Delusion is made up of three factors:
- Most teachers and school leaders think they know what makes great teaching, but they don't;
- Most teachers and school leaders think they know what it takes to improve teaching, but they don't;
- Most teachers and school leaders think that teaching in their classroom/department/school is good enough, but it isn't.
On that last point, Robertson (and I) are very clear that there is poor teaching in schools, but this is not due to a lack of effort on the part of teachers, but rather a consequence of the first two parts of The Teaching Delusion. A lack of knowledge about what makes great teaching, and a lack of knowledge about how to improve teaching have left many teachers doing a good job, when they could be doing a great job, and a smaller minority doing a poor job when they could be doing a good (or great) job. This book is not an attack on teachers or school leaders. It is a realistic look at what happens in many schools, and more importantly, a road map to addressing the three issues it identifies.
"Hard work and effective teaching are not the same thing. Neither are hard work and effective leadership." |
Robertson uses the first chapter to draw attention to what he sees as the issue in most schools, and put together the case for there being a Teaching Delusion. He takes time throughout the book to clearly set out his thoughts on what would improve the situation, which I will go into further below.
In chapter 2, he starts by talking about the purpose of schools (a dangerous topic, but one in which he and I agree), stating that the main purpose of schools is "supporting, challenging and inspiring our young people to learn". Then he gives an overview of some ideas from the research and reading he has done over the last few years, that will be building blocks for later in the book. In this section he attacks some 'myths' such as interpretations of Blooms Taxonomy and student-led learning, before making the assertion that great teaching is made up of a mixture Specific Teaching (explicit instruction, if you will) and Non-Specific Teaching (student led activities, Mode B as Tom Sherrington calls them), but that the balance of these is important. For Robertson, 80-90% Specific Teaching is the optimum, as "Specific Teaching can be thought about as the cake; Non-specific Teaching is the icing".
"As a reaction to their experience of poor teaching, their solution is to minimise the role of the teacher in teaching and learning processes and maximise the role of students. Accordingly, they advocate the importance of students leading their own learning." |
Chapter 3 is an exploration of "The science of how we learn", and Robertson works through 7 keys ideas:
- Knowledge - everything is built upon this
- Memory - how working and long term memory work
- Thinking - "Thinking is the interaction of knowledge, from our environment and our long term memory"
- Learning - a change in long term memory
- Retrieval - retrieving memories strengthens the memories
- Understanding - see quote below
- Schema - complex knowledge constructs
"Understanding happens when knowledge takes on meaning. When we experience new knowledge, whether or not it has meaning to us will depend on the knowledge we already have. In other words, the more knowledge we have, the more likely we are to understand something new." |
In chapter 4, Robertson starts to build toward implications for actual teaching. This chapter acts as a brief summary of ideas from a variety of sources in this field, including:
- What Makes Great Teaching, Robert Coe et al
- Formative Assessment, Dylan Wiliam
- Effect Sizes, John Hattie
- Principles of Instruction, Barak Rosenshine
- Why Don't Students Like School, Daniel Willingham
At this point, we get the first glimpse of Robertson big picture: a description of great teaching.
"I suggest that great teaching is that which typically focuses on teaching knowledge, using pedagogies which are best for teaching knowledge (direct-interactive instruction and formative assessment), by teachers who have a strong knowledge of what they are teaching and how students typically think about this, and who develop strong relationships with their students." |
Robertson then splits the remaining chapters into two broad categories, though they are interweaved so do not appear consecutively. For the purpose of this summary, I have put them into the broader categories. These address parts 1 and 2 of The Teaching Delusion that Robertson described in chapter 1.
Great Teaching
We start with the assertion that high-quality student learning has two main factors:
- Great teaching
- Hard work on the part of the student
"Great teaching requires deep knowledge and skills in relation to pedagogy." |
After some discussion of what great teachers have in common (their attributes), we get to what will form the meat of this section, a list of 12 components of high-quality lessons, which are "the delivery units of great teaching". In brief, these 12 components are:
- Activities that require students to recall knowledge from previous lessons, which may or may not be relevant to this lesson, but which needs to be learned as part of the course;
- Clear communication and use of learning intentions and success criteria;
- Activities that allow the teacher to find out what students know or can do already (in relation to what is being taught in this lesson);
- Clear teacher explanations and demonstrations which hold student attention;
- Activities that allow students to put into practice what they are being taught;
- Appropriate levels of support and challenge;
- Use of questions to make students think and to check for understanding;
- Activities that get students to discuss and learn with other students;
- Clear feedback to individual students and to the class about their learning;
- Activities that evaluate the impact of lessons;
- Strong teacher-student relationships;
- High expectations and standards for student behaviour and quality of work.
I do have a minor disagreement with Robertson here. Whilst I accept that lessons are the practical time we spend teaching things, I am not sure it is useful to think about teaching in terms of lessons. I subscribe more to Mark McCourt's idea of a learning episode which will take as long as it takes. That is, I will prepare resources, but if they spill over into the next lesson, then that is fine. Similarly, if we get through them quicker than expected, I have more available to move on to the next piece of the puzzle. So whilst I agree with the elements, I am not sure I agree in the wording of talking about great lessons.
Robertson then uses the remaining part of chapter 5, along with chapters 9 and 13 to delve into each of these in detail. I am not going to comment on all of them here, but I am going to give some personal reflections on my own teaching.
1. Recalling knowledge - I have become quite systematic in how I approach this. I discussed how I am tracking and Spacing Key Facts, Skills and Concepts, and I will be starting to do this with all my classes next year. Prior to that I used the Last Lesson, Last Week, Last Unit, Further Back approach which also worked well, but I found that I missed out some ideas, especially in the Further Back section. I need to figure out how I am going to build this in to the spreadsheet (content covered in previous years when I haven't taught them). Since going on lockdown I have also dropped the weekly quizzes I used to do, simply because of time pressure. I am planning to build in some more smaller quizzes, perhaps only 3 questions a lesson, which should also have the benefit of breaking up a long lesson on Zoom.
2. Learning intentions and success criteria - this is an interesting one, and one of the few things where I disagree with Robertson. I do not believe that students need to be shown the learning intention, but I certainly agree that they should be at the forefront of teacher planning. My use of Booklets and Lesson Sheets have really helped me to do this, both in the curriculum planning when putting them together, and in individual lessons.
However, I can see the benefit to having these explicitly stated, and I think I will add them to my booklets and sheets, following the advice that Robertson gives, using the phrases "Will know", "Will be able to" and "Will understand". But then I will have them all available, and refer to them as we get to them, rather than at the start of a given lesson. Referring back to learning intentions reminds me of the Learning Map that Jim Knight discusses in High-Impact Instruction that I have been playing around with. I could adapt this to map the learning intentions perhaps, but I need to think more carefully about how I will go about this.
Success criteria is more interesting, and whilst I once again disagree that they need to be made explicit to students (in my subject anyway), having a clear question that can be asked to evidence their performance against would be useful. Again, this is something I can easily build into the booklets and sheets, having 1 or 2 questions at the end of each section which all students do before moving on. This would be a little like an exit ticket, but they would not appear at the end of a lesson, but rather when we get to them.
4. I have been thinking a lot more carefully about the questions I use as examples in recent years, ensuring that I show students the full breadth of a concept, including non-examples and boundary examples. But I have not focused as much on explanations. There is an argument that giving a good explanation is what separates a teacher from a subject expert: they both know their stuff, but not every expert can explain this to others, especially kids.
"It is often quite striking to me just how many teachers are reluctant to actually 'teach'." |
I want to keep developing my example sequences, in line with some of the ideas from Engelmann's Theory of Instruction (Summary by Alex Blanksby here), and delve deeper into that text to explore the order of examples and non-examples in different contexts.
5. Practice is so vitally important, and in Maths especially so. Students need to practice methods to gain fluency, but also different types of problems to develop flexibility in their thinking around an idea. But this is always the first thing to get cut from my teaching when the time pressure hits. The pressures of "covering the curriculum" can get to us all, and I know that when they get to me, this is where I cut corners. Unfortunately we have lost time with all year groups in the last couple of years, so this is even more of an issue now. I need to make more use of homework tasks to get students practicing their new knowledge and skills.
8. I am not a fan of group work. It rarely works for me, and even when it does, there are always some who just sit to one side and get nothing from it. For this reason I have swayed too far away from it. I need to give students structured ways to work together, and Think-Pair-Share seems to be the most appropriate way to do this. I ask a question for students to do on their mini-whiteboards, give them time to complete it themselves, then share with their partner. In Reflect, Expect, Check, Explain Craig Barton gives some examples of prompts he used to get students following the structure he has developed, and something similar for Think-Pair-Share could be useful, until it becomes habit for students and me!
Improving Teaching
"Teachers are unlikely to improve a particular element of their teaching practice unless attention is drawn to the fact that they could be improved or need to improve." |
The other main part of the book is about improving teaching, and creating a "learning school". It is based around the idea discussed at the start of this post, that all teachers can improve their practice, and so should be doing so.
"learning should be the core business for everyone involved in the life of a school - students, teachers, school leaders and support staff" |
There are two interesting scales that schools need to think about when thinking about improving teaching:
- Professional autonomy
- Consistency
These are clearly linked, though they are separate (high levels of professional autonomy may result in low levels of consistency, though depending on how it is managed, this is not necessarily true). There is no correct place on these scales, but having the discussions as a school is important. Are there things we want to be consistent about? Behaviour is one area where most agree that consistency is important, but what about pedagogical choices. My personal view is that a certain amount of consistency amongst teachers would make everybody's life easier: students would need to spend less mental effort thinking about what each teacher wants; teachers do not have to come up with their own systems, and students develop the habits more widely so can apply them better in every class.
As to Professional autonomy, I believe that this should be high: teachers should be in control of what happens in their classrooms and in their professional learning. But I do not believe that "teachers should be left to get on with the teaching" in a vacuum. The role of school leaders is to oversee the productive learning of teachers, just as it is a teacher's role to oversee the productive learning of students. How these are approached differs in the fact that students are (relative) novices, whereas teachers are (relative) experts as professionals. And Robertson goes on to describe what he calls a "Professional Learning Culture", which basically means that a school (leaders, teachers, administrators) sees professional learning as important.
In such a culture all teachers are working to improve, and they do so in a collaborative way. When somebody learns something new from reading, it is shared amongst other members of staff. Teachers observe each other and give each other effective feedback. Teachers feel confident to try new things, without fear of repercussions should they go wrong (within reason, obviously). Teachers participate in discussions, reading groups and collaborative planning as ways to learn from each other.
In building a Professional Learning Culture, Robertson argues for a group of teachers to lead it. This is something we do not have. I act alone in leading the T&L Programme in our Upper School, in semi-regular communication with my counterparts in other sections. One thing I want to do soon is set up such a group within the Upper School. This would be a group of keen teachers to help plan the T&L Calendar, run activities, and possibly most importantly, act as ambassadors for the benefits of getting involved. Ideally there is a mix of leaders and teachers in this group, and my plan is to open it up next term.
This sits alongside the Professional Learning Evaluation survey that Robertson supplies. I have copied this off to give to our Management Team for them to reflect and evaluate how they feel we meet against these ideas. I will then be passing this survey to all teachers next term, and it will be interesting to see the different viewpoints from staff at the different levels. My suspicion is they will be quite different, but we will wait and see.
And now to what I found to be the most interesting and useful part of the whole book: the Lesson Evaluation Toolkit. Robertson sells this as a key part to developing a culture of improving teaching, as it can be used in many ways:
- Building a common understanding of great teaching
- Self-evaluation of lessons
- Planning of lessons
- Focusing feedback in observations
- Peer observations
- Focusing INSET sessions
It is basically a list of the elements of great lessons as identified by the school, with examples of their use and a space for teachers to take notes. I go into further detail about where I am going with this idea below, linking the idea to The Principles of Great Teaching.
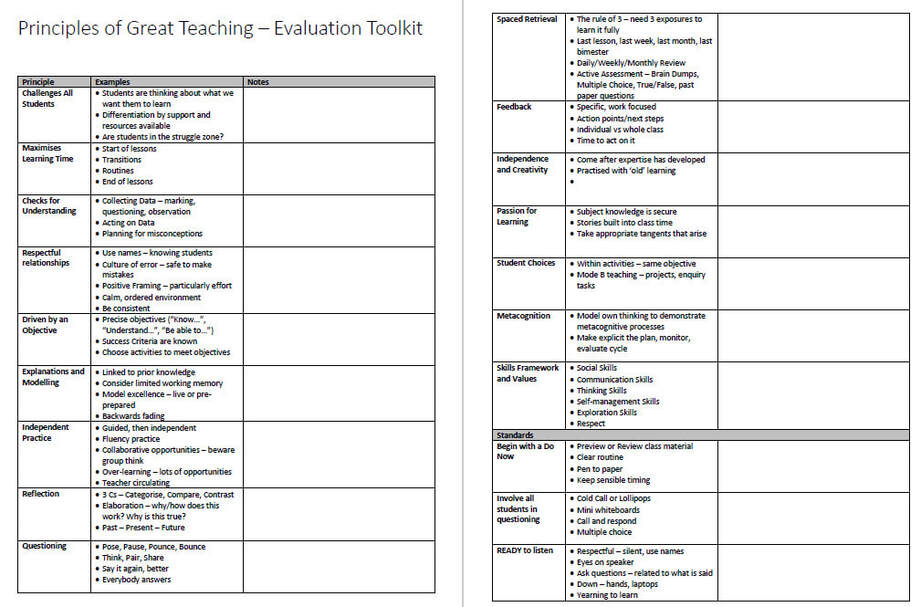
"Use of the Lesson Evaluation Toolkit in lesson planning is not about making all lessons look the same - it is about getting all teachers to think about the same pedagogy as part of their planning." |
The main way to deliver good and improving lessons is through careful planning, delivery and then evaluation of the lesson afterwards. The Lesson Evaluation Toolkit can be used in both planning and evaluations. In planning teachers could have a copy to hand whilst planning, so they can refer to it. Or they could go further and plan on the document itself. After a lesson teachers can ask themselves evaluation questions, and give themselves a rating (red/amber/green) against the elements of the toolkit, along with some brief notes. This process of evaluation is what is important, rather than the finished sheet (which could be thrown in the bin). By sitting down and focusing on evaluating a lesson, a teacher thinks about what went well and could be repeated again, and what didn't and they need to work on for next time.
Another key part of improving teaching is to make use of lesson observations. There are two broad types of lesson observations:
- By a leader (to provide useful feedback to the teacher, to provide feedback to the leader about areas of development, and NOT as a way to make judgements)
- By a peer (to inspire the observer, to provide feedback to the teacher, to share good practice)
"I actually believe that giving feedback to teachers about teaching practice is one of the most important things that school leaders can do with their time." |
In either case, lesson observations must focus on professional learning. And even if they do, there are still reasons they may not have much of an impact on improving teaching practice, usually related to the issue of feedback. Robertson suggests 4 reasons why feedback from lesson observations does not lead to improving teaching:
- No feedback is given to teachers;
- The feedback is poor;
- The person giving feedback isn't confident about delivering it (that is, it is delivered poorly);
- Nothing is done with the feedback.
"Use of your school Lesson Evaluation Toolkit can help to create a degree of consistency in the feedback given to teachers following an observed lesson." |
The first three can all be addressed by using a lesson evaluation toolkit as this provides a structure to giving feedback. With a defined toolkit, all feedback should be given in relation to these, and it also allows for feedback meetings to be more of a discussion as the teacher can also reflect on the lesson in terms of the toolkit. In particular, when feedback is specific and related to an agreed area of focus, the teacher is more likely to act on the feedback. This is where coaching can fit in as well, as coaches can work with teachers to implement the feedback. We are currently implementing a coaching programme at Markham College (…) and I can see the place of the Growth Coaching model following a lesson observation to help a teacher work through how to make the feedback impactful on their teaching.
Robertson also goes into the details of how to run effective lesson observations, and what the observer needs to do to make it useful. In particular, he suggests that an observation should be as much work for the observer as it is for the teacher, as they should be thinking hard about what they are seeing, and whether it matches up to the lesson evaluation toolkit.
"If you try to improve too many things at any one time, the likelihood is that you won't improve anything, certainly not to any significant extent. " |
Next Robertson moves on to think about planning schoolwide improvement, and the quote above is given in that context. However, it is also true of individual teachers improving their teaching. It is important that when feedback is given to teachers following a lesson observation, only one or two target areas are highlighted. The observer should sit down and go through their notes before giving feedback in order to clarify what feedback they are going to give, and what areas of improvement they are going to suggest. If the observation was done as a pair (something Robertson suggests is useful), then the observers should discuss their notes together and come up with an agreed set of feedback.
Back to schoolwide improvement, of particular interest to me was the idea of collecting data about the areas on which to focus improvement. Without data, school leaders are focusing improvement planning on what they think are the biggest needs, but they may be very wrong. Data allows us to be more sure that what we are doing is a) needed and b) making a difference. Robertson gives an example of a simple spreadsheet which can be used to record data from lesson observations. The idea is that leaders observe lessons (ideally in pairs), then after the feedback they record a simple Red, Amber, Green in the spreadsheet against each element of the lesson evaluation toolkit. Over time this gives leaders data on two things:
- Areas of weakness across the whole school, which should then inform further improvement planning;
- Areas of strength of particular teachers, who can be used as examples for other teachers to learn from.
"the overall quality of lessons is not being evaluated. Instead, it is specific pedagogical elements of lessons that are being thought about, as identified in the school's Lesson Evaluation Toolkit." |
This process could be used at a whole-school level, or within departments. I would say there is an argument that the latter is a better way to approach it, because elements of a lesson evaluation toolkit will probably look quite different in different subjects. This data could also be collated on a whole school level to focus whole school CPD.
The other main type of data that can be used to inform improvement planning is student feedback. This is probably best if given straight to the teacher and not via leaders to make sure that teachers don't feel like they are being "checked up on" by students.
"it is important that the focus is on improving the 'right' things. Without a focus on the right things, teachers and school leaders will be working hard but their efforts are likely to be in vain." |
Robertson offers the acronym PACE to help maintain focus on the 'right things'. The acronym stands for:
- Pedagogy
- Attainment
- Curriculum
- Ethos
Finally, Robertson turns towards leadership in school, and he argues that school leaders should take a teaching-centred approach to leadership. The vital importance of knowing where you are going and communicating this to teachers is explored with the analogy of a driver in a car with passengers where the driver either will not tell the passengers where they are going, or does not know and is just out for the drive. Whilst the passengers might initially go with it in both cases, they will eventually get fed up and probably start to mutter in the background.
The teaching-centred leadership approach puts improving teaching at the heart of what a leader does, with the intended outcome of this being improved student learning and outcomes. Robertson identifies 5 reasons why many leaders are not teaching-focused:
- Too much time is spent on other priorities
- Too much time is spent on 'dealing with things' which could be dealt with by others
- They don't know how to improve teaching quality
- They believe that teaching is good enough
- They believe that teachers will take care of their own improvement and that leaders don't have a role in this
So what should teaching-centred leaders be doing?
- Make improvement of teaching the number 1 priority
- Develop a shared understanding of great teaching
- Focus professional learning on pedagogy
- Lead by example
- Read a lot
- Observe lessons a lot
- Support and challenge teachers to improve
- Make time for people
- Take different approached with different colleagues
- Recognise strengths and good practice
- Have difficult conversations when necessary
- Talk about teaching and learning
- Invest time and resources in collaborative professional learning
- Plan for improvement taking into account data
And this is the message that Robertson finishes with. A focus on improving teaching being the main job of school leaders.
The Lesson Evaluation Toolkit and The Principles of Great Teaching
As I read about the Lesson Evaluation Toolkit, the first thing that came to my mind was that we have one of those. A couple of years ago I led a team in putting together what we have called the Principles of Great Teaching, and the purpose of this was to create a shared language around great teaching, focus our T&L programme, and make it easier to share great practice and expertise. But so far we have not been super successful in this goal, and there were several parts of this book that has helped me realise why.
The first thing I did on reading about this was to turn our Principles policy document into a toolkit like document, that is hopefully more usable by teachers. I have largely followed the structure recommended in the book to do this.
What must be made clear is that this is not a tick-list of things that are expected to be included in every lesson. In fact, we talk about these being Principles of Great Teaching rather than Lessons for that very reason. Over a period of time, we would expect that these Principles will appear, but certainly not in any single lesson. The more a teacher uses this to self-evaluate, the better the picture they will get of how well they meet these Principles. The exception is the first four which we call the Core Principles, which are expected to be in every lesson.
"A push for a shared understanding of what great teaching is and what typical features of high-quality lessons are is not the same thing as a push for every teacher to teach in exactly the same way." |
The second point is that these are Principles and not specified activities. We expect teachers to challenge students, but we do not specify how they should do this. This is the idea of "freedom within form", and the balance of Professional autonomy with consistency I referred to before. Again, there are 3 exceptions, the Standards at the end, which are more specific things we want to be consistent throughout the school. There is still room for teachers to make this suit their own classes, and one error that we originally made was having the second Standard worded as "use a no hands up policy" where that is really a specific example of the idea we wanted to promote.
I said above that we have had some issues with rolling the Principles out successfully, and partly that is because our teachers still do not have a shared understanding of what each of these things means. My hope is that by turning it into the Evaluation Toolkit we can get it into teachers hands and get them using it more regularly. As teachers use it to reflect on their lessons, as teachers meet with coaches to discuss their teaching in relation to the Principles, as leaders start to use it to reflect on the practice within their department, teachers will become more aware of the different Principles, and they will be forced to engage with what they mean. Carefully planned whole school and department sessions will then allow us to see what different people think, and slowly build towards a shared understanding. This is not going to be a quick process. As an international school, we have teachers who have been trained in various different countries and so have very different ideas about education, and so all these ideas need to brought together.
But it will be worth it in the end. I have to keep reminding myself of that. In the end, this will lead to better teaching and thus better learning, and that is what is important.
How do I see this being used moving forward?
The first thing I am planning to do is to sit down with some departments and ask them to reflect on the department as a whole using the Evaluation Toolkit. This will hopefully spark some discussions, and through a coaching process, I hope to get them to move towards a departmental goal within the framework of the Principles, and how they can work towards this. Working with a few departments, especially some of the bigger ones, will get the language of the Principles in discussion with a large number of staff.
Following this I will be talking with the coaches we have trained over the last year, and asking them to guide teachers to this document where appropriate. Especially within the framework of instructional coaching, this will give teacher and coach a framework to identify the current reality, which is a vital part in identifying a goal.
Then I am hoping to start doing more observations of teachers. In the last couple of years I have focused more on Learning Walks, but I think seeing whole lessons will be helpful. This will give us a structure to base feedback upon, and if I can get Heads of Department to use it when observing their teachers it should lead to more productive feedback meetings following the observations. This will then hopefully lead to teachers engaging in Peer Observations, making use of the Principles Evaluation Toolkit to structure feedback.
We put our collaborative projects on hold for a couple of years because there were some policy items that took up a lot of time (the introduction of the IMPACT course, which is a skills based curriculum, and then the new national curriculum and assessment regulations introduced in Peru this year), but I am looking to bring them back next year, with a focus on the Principles, where teachers will choose to work in a group that focuses on one of them.
Within INSET sessions (we have one every Wednesday 3:00 - 3:40), I will plan sessions which are dedicated to reflecting on our teaching practice, and for these sessions I will provide all staff with a copy of the toolkit to make notes on.
All this will hopefully (fingers crossed) lead to staff seeing the toolkit as a useful document to scaffold their thinking when it comes to planning lessons and reflecting on them.
The end goal is that teachers are using it to reflect on their teaching regularly, but how it is used in those individual cases will not be dictated. It is, after all, a toolkit, and teachers need to decide how to use it that is best for them. But, by having lots of exposure to it through a variety of linked ways, I am hoping that teachers will start to develop the shared understanding of what makes great teaching, and the document will evolve with that understanding.
RSS Feed
