|
In a recent lesson with my IB Maths AA SL class, I set them this indices question to simplify as part of the starter activity. They struggled. A lot. Since teaching via Zoom, I don't usually go through these retrieval based activities in class straight away, rather opting to take in their work to check through all their work, which gives me a better idea of what they can and cannot do (in a classroom it is different as I can see their work live). Very few of them got anywhere near close to solving the problem. In the following lesson, they asked me to go through it, so I did. After showing them how to do it, I made a passing comment about enjoying doing this kind of problem, even finding it relaxing. Even via Zoom, I could tell the reaction of my students. Some of them even turned their cameras on to show their disbelief. How could I enjoy solving this kind of problem? How was it even remotely relaxing? This provoked a rather interesting discussion where we talked about the things we find enjoyable. My point was that when you can do something, but it requires a bit of work, that is normally what we find fun. That is, learning is fun if you know enough to be able to learn. We discussed how some people enjoy music or sports, and the reason why is normally they are relatively good at it. And then they enjoy getting better and doing more difficult aspects of that course. It is the same with Maths (and anything else really). If you are constantly failing at it, you will not enjoy it. But if you can do it, with a bit of effort, normally you will enjoy it. They could understand this point. I don't think they had ever really thought about why they enjoy some things and not others, and it helped them see how I could enjoy solving a Maths problem. I told them that my job was to help them know enough that they could enjoy solving Maths problems. Now I just need to live up to that!
2 Comments
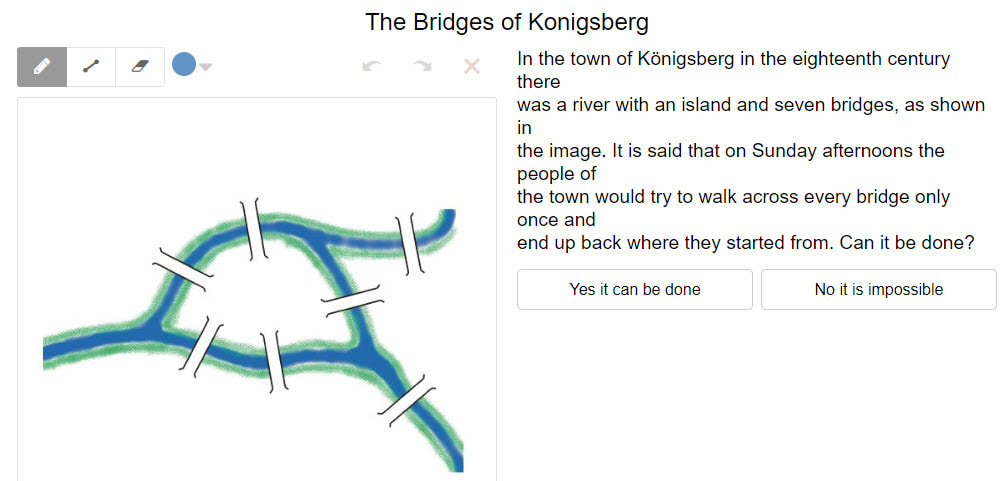
Due to COVID-19, we are unable to run our IB and IGCSE exams this November. Local restrictions make it impossible. It has been tough for students and teachers to have 2 years worth of work count for nothing. Our students will not get an IGCSE set this year (as an international school, no systems in place like there were for the UK). The IB students will have grades awarded purely on coursework. The announcement that there would be no IB exams this year was made the day before I was due to finish teaching the syllabus, and my IB HL class were keen to finish that last little bit of vectors. But we still had two weeks left of term left, and with no exams, the usual rush of exam papers was pointless. So between me and the other HL teacher we decided to offer two separate options: she taught the calculus option (we did a different option, but many students were interested in this) and I did a series of lessons on random mathematical diversions. Here I will share those diversions, along with the resources, in case anybody ever feels like using them. Taxicab numbers We started by looking at this problem. I blogged about this problem in the past here when a student brought it to me. I ran the session basically as an open problem, with students in breakout rooms in Zoom, and me popping between them. Benford's Law Next we took a look at Benford's Law. I asked students to think about a set of data. They could choose anything, but I gave some ideas like
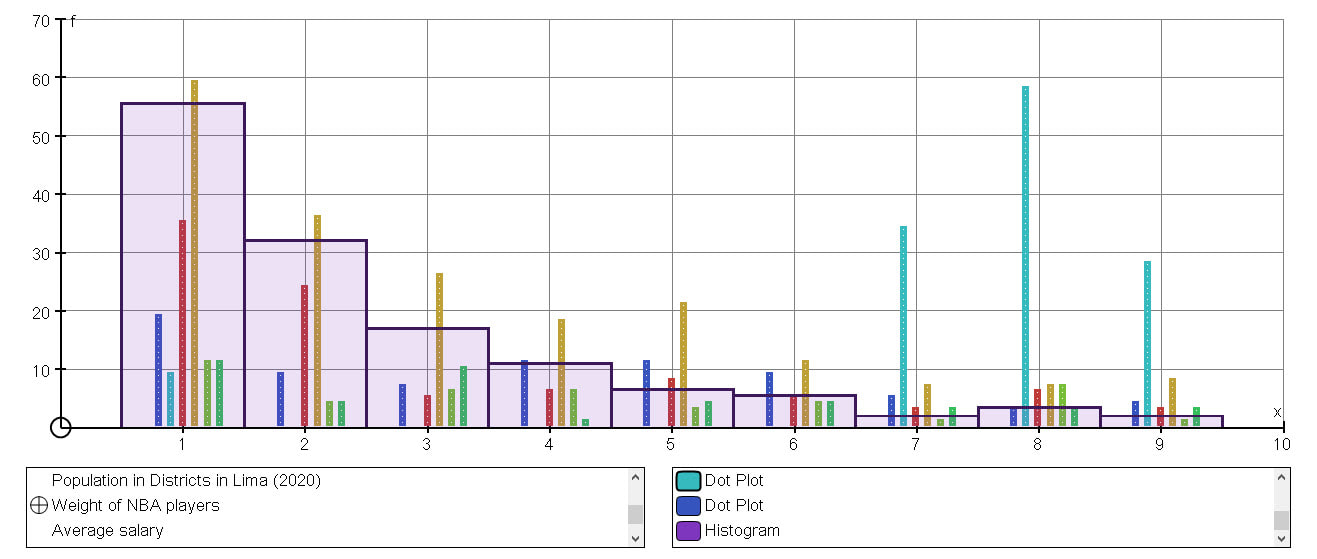
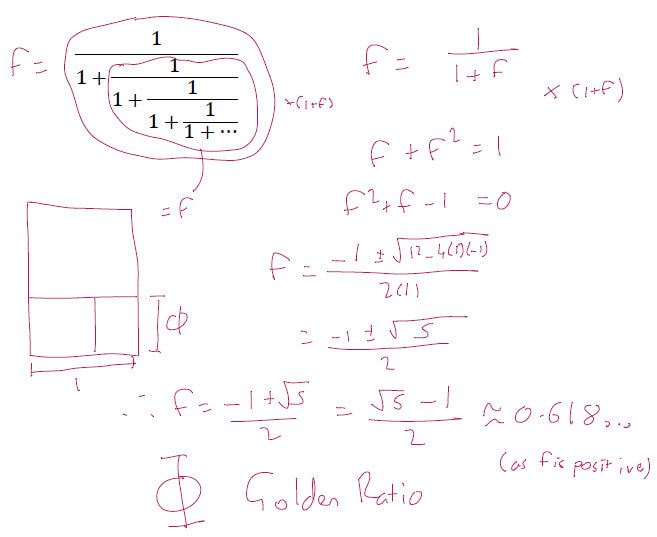
Once they all had an idea of their data set, I asked them to think about the first digits of each data point in the set, and to decide what the probability distribution would be for them. That is, what is the probability if you choose a random point in your data set, the first digit is a 1 (or 2,3,…) We had a brief discussion about this, with the first answer being the expected 11% each as they are all equally likely. One student suggested that they would be clumped around a number (probably the mean) value. After a brief discussion, I told them to go away and find the data set they had thought about in the first place. We entered them all into this Google Sheet. And then I added the data sets one by one to Autograph. Obviously, with any activity like this you are open to it failing dramatically, but below you will see all the data sets plotted together, and Benford's Law falls out beautifully. There is even an excellent non-example. The non-example was of weights of NBA players, and we discussed why this did not fit the pattern (weights will all fall within the range 70 - 120 kg approximately, so the first digits will be 7, 8, 9, 1, and the mean is in the 80s, so more 8s as this is a normal distribution. But what about the other data sets? Why do they follow this same pattern? I finished the session by explaining Benford's Law, the percentages it predicts and the formula, and how it can be used to spot people who have made up a data set. Exploding Dots Exploding Dots was a part of the Global Maths Project a couple of years back, set up by James Tanton. It is definitely worth checking out the website. However, I prefer to teach it a bit more actively, and so created a version that I can present to students, with questions for them to do along the way. You can find a blank PDF of this here. It starts from the very beginning of school level Maths, with counting (in different bases), followed by the four operations. It introduces the idea of zero pairs to perform subtractions, and then builds up to unknown bases: that is polynomials. Within an hour you can take a group from counting to performing polynomial divisions. I have done this with other classes before, and it went down well with this class too. By the end of the first double period we were answering questions like the one below (admittedly, they do this in the course, but we did the more traditional long division). We took this further to polynomial division that creates infinite polynomials, and the students wondered what would happen in other situations. It was so popular, that we did a second double period on Exploding Dots, and this was all new stuff that I hadn't done with classes before. We looked at decimals and fractions in the exploding dots model, which allowed us to look at fractions in different bases. Then we looked at fractional bases, and explored what they might look like. I love the exploding dots model. The students all commented on how visual it was, an how easy it was to understand what is going on. I really need to make more of this in 'normal' teaching, and not just as an enrichment activity. Bayes Theorem We study this in the course, but a couple of students asked to look at it in more detail. I was fairly lazy with this one, relying on some excellent resources available online. First I sent students to this page to read the examples. We discussed the importance of the size of the population, and then did a few of the questions at the bottom of the page. Then we watched this excellent video from 3Blue1Brown which visualises the whole thing beautifully. Chinese Postman I taught D1 once before leaving the UK, but it has been a while since I have done any decision maths. I thought this was a wonderful opportunity to take a look at the Chinese postman problem. I based the lesson on the plan from the Standards Unit, and turned it into a Desmos Activity. It was a very discursive session, so I paced them through the activity to start with, and also talked about the ideas whilst demonstrating and collating their ideas on a whiteboard. Continued Fractions Based on a couple of articles from nrich, I put together an activity on continued fractions. We started with evaluating them (like the one below). We quickly moved on to look at infinite continued fractions And generalised this We took a quick look at how we can write any rational number as a continued fraction by using reciprocals. And then how we can use continued fractions of surds to get pretty good rational approximations for them Finally we took a look at some of the continued fraction representations of other irrational numbers such as pi and e. It was fun to get to explore some different aspects of mathematics with the class. I really must try to build it into my teaching more often, and not as enrichment, but as an integrated part of teaching Mathematics. If you have any go to activities like this, I would love to hear about them.
|
Dan Rodriguez-Clark
I am a maths teacher looking to share good ideas for use in the classroom, with a current interest in integrating educational research into my practice. Categories
All
Archives
August 2021
|
|
Indices and Activities
|
Sister Sites
|
©2012-2023 Daniel Rodriguez-Clark
All rights reserved |
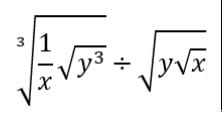




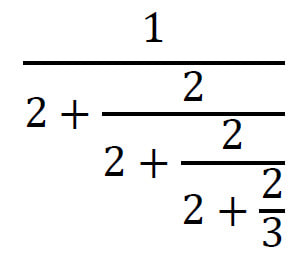

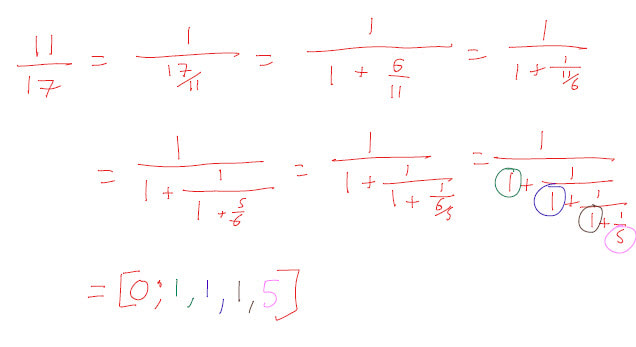

 RSS Feed
RSS Feed
