Our students are currently heading towards their mock examinations, and usually at this time of year I do an assembly with them to talk about effective revision. But this year we are all on lockdown due to COVID-19, and it seems unlikely that we will be back in school any time soon. 

So I decided to do something I have meant to do for quite some time: put together a brief guides for students and parents on how to revise effectively. I wanted to build in the elements that I usually present, which are all evidence informed, and present it in a way that would help students identify both why it is important and what they should actually be doing.

I have seen other similar ideas before (a couple are linked in the Further Reading section), and there is nothing groundbreaking in what is included. Mine is just another example that people might find useful to share with their students, parents and colleagues.

You can find a PDF version here (and the one with my school logo here) .

I used to have a classroom full of displays. Common misconceptions, etymology, the Maths Mr Men, historical problems, a challenge corner with problems of the week. I even had bunting. But over the last couple of years I have really started to rethink the design of my classroom. Mostly inspired by the ideas from Cognitive Load Theory, I started to think that displays might actually be distracting, and, as Craig Barton has said, the cognitive effort required to ignore them takes up working memory space.

Recently I read this piece from Mark Enser on the TES also about classroom displays, and he argues a similar point that they could cause more harm than good.

So I thought I would share what my classroom looks like at the moment.

The front of my room has a SMART board in the middle, with two whiteboards on each side. We have adopted as assessment criteria around the Approaches to Learning Mathematics, and the rubric for this is on the board on the right (Engagement & Curiosity, Perseverance & Resilience, Independence & Reflection, Mathematical Communication, Resourcefulness, Academic Honesty). I also have a small poster of my Eight Tips For Learning Maths document, which I give to all students at the start of the year. Above the door I have my favourite edu-quote: Memory is the Residue of Thought, Daniel T. Willingham.

I have had all the display boards removed from the side of my room, and now have three big whiteboards, which I often use to get students working on problems. I have the posters from the Learning Scientists which I refer to when teaching students study skills. I also have a copy of my classroom expectations document, which I hand out to all students at the start of the year. In the back corner is the quote "Practice Makes Permanent, Anders Ericsson".

UPDATE
​I have since removed

The other side of my room is similar with two big whiteboards (I have asked for a third to go in the middle), and two quotes: Learning Occurs Over a long time, Hermann Ebinghauss and Our Working Memories are limited, John Sweller.

UPDATE
​I have been working with a group of teachers on checking for understanding, and we have defined 6 stages of understanding. The next stage is to start referring to these to help students be aware of their own level of understanding. To do this I have put up an extra display.

I have lovely windows across the back wall of my room which look out onto the school field past a small bio-garden used for activities to grow things. The tree is home to a hummingbird. I have a set of shelves where students can leave their textbooks and folders, and I keep extra exercise books, scrap paper, mini whiteboards, and printed templates of some regularly used activities (exit tickets, two truths and a lie, frayer diagram, question reflection sheets, etc). I will blog about these at some point soon! The clock is on one of the pillars so I can see it, but students cannot (without turning around). This avoids time-watching being a possible distraction.

The most cluttered part of the room is my desk area, and it needs a good clear out! It is the end of term , so please forgive the mess! But I have my desk, with an extra desk next to it with my visualiser on. Behind me is my shelves with my paperwork and books. On the walls around my desk I have some notes to myself, copies of my summaries of research, extracts from the T&L Newsletter and the Principles of Great Teaching document. As well as a few personal bits like photos of me with my son, etc.

I have already been rethinking the area around my desk. There is a lot of stuff, and lots of it is not needed. Even the stuff on the walls, I rarely actually refer to, so I think I will be taking some of that stuff down. I have also thought about taking down the Learning Scientists posters (as much as I love them) as they are too small to actually see. I refer to them sometimes, but students never really look at them, so do they really serve the purpose I had hoped. Similarly with the expectations and tips for learning. I either need to get them printed larger so they can actually be seen, or just get them in the front of books/folders, and refer to them there.

I almost exclusively have my desks in pairs (sometimes regrouping into groups of 4 on rare occasions). This allows students to discuss ideas with their partner, but means all students can see the board easily. It also gives me ample space to move around the room, and I can crouch next to or in front of every student in the room (with the exception of next to those beside one of the columns).

The four quotes are new this year, and I have found myself referring to them quite a lot. I talked about the ideas at the start of the year with my classes, and when appropriate now, I can just point to the quote. I deliberately only had one on the front wall, but maybe I need to move that to a side wall as well?

There is some space on the back wall below the windows, and I have been thinking about putting a Mathsy display up there. Something fun and interesting. Being on the back wall it would not serve as a distraction, but could add some more "life" back into the room. But I am not convinced yet.

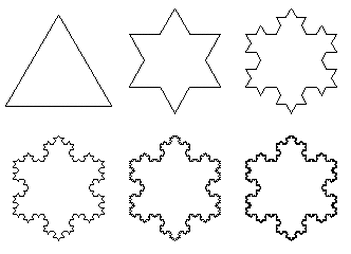
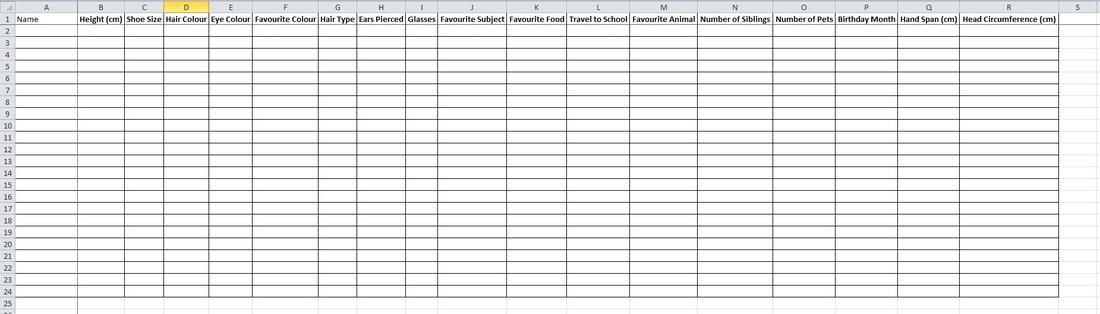
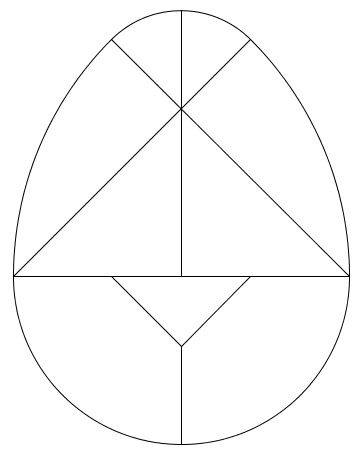
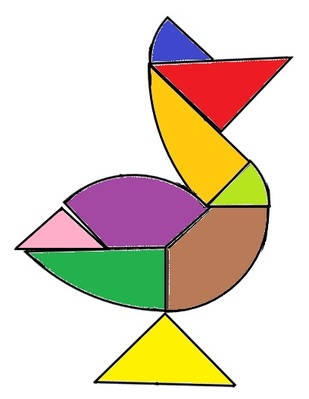
This year with my Year 10 class I decided to build a fractal christmas tree as given on Think Maths. However, before getting into the making, I wanted to explore the world of fractals with the class a little bit first.

I started by looking at the Koch Snowflake, and we found this by constructing it. We started with an equilateral triangle that had side length 9cm (a little revision of constructions), and then split each side into three 3cm sections. On the middle of each of these sections, we constructed a new 3cm equilateral triangle. Now we split each 3cm side into three 1cm sides, and again constructed a 1cm equilateral triangle in the middle section on each side.

We then discussed the nature of fractals and their self-similarity, and their applications to things such as coastlines.

With open day fast approaching, it has been that time of the year when all the displays get a revamp. I like to do lots of posters and displays anyway, but in the run up to Open Day, I wanted to something a little bit special. And this year I devises a project for my Year 7 class which ran over a couple of weeks on the different types of numbers.

We had started by looking at various types of numbers, starting with the usual suspects such as Primes, Factors, Multiples, etc. But we diverged into some other nice types of numbers as well, such as Perfect Numbers and Happy Numbers. I used this PowerPoint (shown below) to deliver the lessons, and talk through the different properties.

With my Year 7 class we have recently been studying various aspects of data handling, including averages (including from frequency tables) and a variety of graphical representations. With the end of term drawing near, and having completed the scheme of work ahead of schedule, I decided to do one of my favourite projects with the: the Average Student (available to download from TES).

This project uses many areas of the data handling cycle, and in my opinion is an excellent way to get them to see the whole process.

Once I had introduced the task to them, we started off by discussing what kinds of information we could collect about the class. There were lots of good ideas, and a few more abstract ones as well, and we started to build up a spreadsheet of all the data that we wanted to include. It is really important (in my opinion) to let them decide which information it is that we should collect to give them more ownership over the task. I would recommend having a few ideas to include if they don't come up with any though. Height, eye colour, shoe size, number in family, etc are good ones, as they cover the different types of data.

The idea of Non-Transitive Dice has been around for a while. The basic premise is that Red beats Blue, and Blue beats Green, so we expect that Red will beat Green. However, as the Non-Transitive suggests, this is not the case, and actually Green beats Red.

There are many sets of 3 Non-Transitive Dice, and one way to introduce them would be to use the trusty NRICH. This introduces the idea to students, and lets them play around with them a little bit.

However, as interesting as the Dice are in themselves, we want to get at the maths behind them.

The video below is of James Grime of the University of Cambridge. He starts by explaining a 3 Non-Transitive Dice game, and goes on to look at a 5 Dice game that he has invented. There is also his full article on the Grime Dice as well. And you can buy an amazing set of the dice from mathsgear.

I love the end of term, as it always brings the chance to dive off the scheme if work a little bit and do something a bit different. Here are a few ideas that I have used just before the Easter holidays, and have always gone down well.

The first is Easter Egg Tangrams. This is a spin on the classic tangram puzzle, where the pieces are made by cutting up an egg rather than a square. Students have to follow some detailed instructions to first create the egg (using lots of compass skills). Once they have the pieces, they have to arrange them to make some different birds.

It always amazes me some of the things you can find on www.tes.co.uk and yesterday I found a real gem. For those of you that haven't read "17 Equations that Changed the World" by Ian Stewart, it is definitely one that you should read.

This wonderful resource sees the 17 equations turned into simple but effective posters. They are eye-catching, and bound to spark the interest of a few students in the corridor. The user who uploaded them suggests they are the perfect way to reply to the age-old question "Why do we need algebra?", but I think these posters have so much more to them. They are of varying levels, and so can interest any secondary age group, and they give students a nudge towards going to look something up themselves, as well as how far mathematics can really take you.

I'm going to be printing them off, laminating and putting them up next week, and I look forward to the responses from the kids.

I know this is an idea that has been around for a while, but as a relatively new teacher, it is the first time I have got round to actually doing it this way. I have done the challenge in class before, but this term I am opening it up to the whole school!

For those who don't know, the Four 4s challenge asks students to use the digit 4 four times along with any mathematical operations to make the numbers 1 to 100. They can combine the digits to make 44, and can use any operations they can think of, including factorials, powers and roots (as long as they make the power using 4's!)

I have put the display in the main maths corridor, which is in a fairly central location in the school. Rather than have students write their own answers on the display, and to allow the activity to continue when I am not there to check and write up immediately, I have come up with a system where they submit their solutions on a named slip, which they hand in to be checked. If correct, I will then add their solution and name to the display for everyone to see.

To add another edge to the problem, I will also be allowing them to submit "better" solutions for numbers which have already been solved. By better, I mean more efficient, which will be measured by the number of key presses on a calculator it takes to input the calculation.

I am hoping that the location and input method will get the whole school involved in the problem, from Year 7 to A-Level. I am also going to award prizes for completing "random" numbers, which I have pre-chosen as winning numbers, but have not told them which ones they are.

I put up the display on the last afternoon of school, after the students left, before Christmas, and I am looking forward to getting underway with finding them all!