|
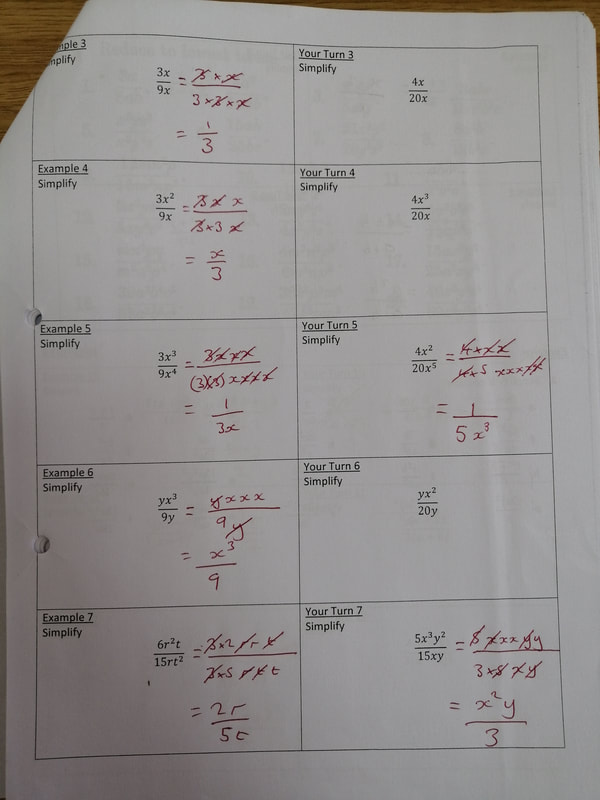
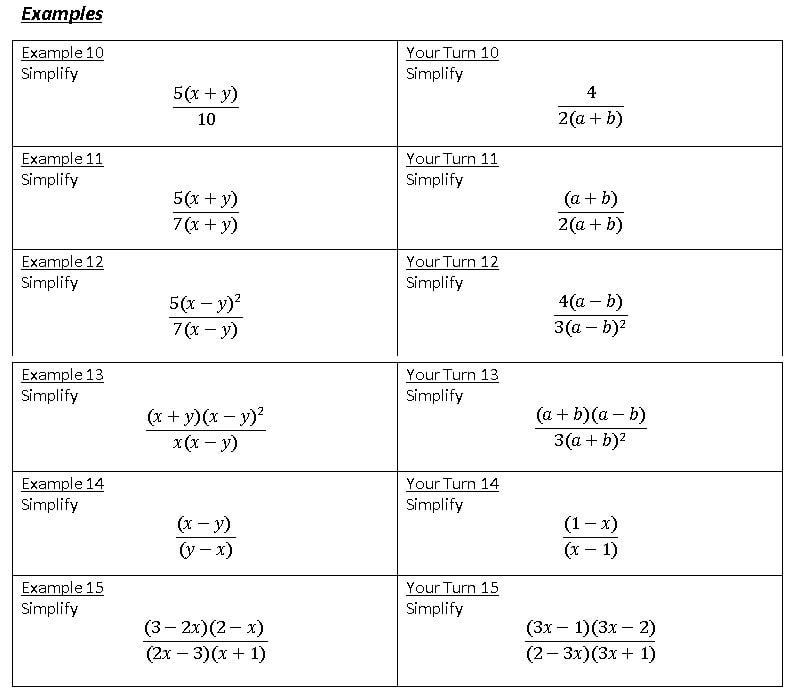
I have been teaching algebraic fractions to my S4 IGCSE class. I am about halfway through the unit, and I wanted to take some time to reflect on how it was going so far. I started the unit by getting students to answer a serious of questions on cancelling fractions and equivalent fractions. I generated these using my website as I wasn't concerned about the order of questions as it was all stuff they had done before. However, in reviewing this, I decided to talk explicitly about what we are doing when simplifying a fraction. I was very deliberate with my wording "We are looking for common factors in the numerator and denominator that we can cancel". In saying this I broke the numerator and denominator into a product of factors, as shown below. We then extended this, with me saying "To simplify algebraic fractions we find common factors in the numerator and denominator which we can cancel." Following this I ran through a series of Example Problem Pairs (shown below). I have started doing this using my visualiser so students can see the layout I use in the booklet they have to copy the examples into. I broke up the numerators and denominators into the factors, then cancelled them (I have always taught spotting these before). There are 9 example problem pairs, showing different types of simplifications they may come across. As this was quite a lot of examples, I didn't want to spend ages going through them all, so I decided to do it quickly. For each example, I called students attention to the board ("Eyes on the board" - I have been working with them for 6 months on how to behave during examples, so this is all that is needed most times), and then I worked the example on my copy of the booklet. They are watching the screen, not talking and not writing. In this case I did not feel the need to narrate after doing the example. As soon as I was finished I said "Your Turn", and all students copied down the example and attempted the corresponding problem. I then Cold Called a student to give the answer to the Your Turn, making an effort to congratulate them for getting it right. In one instance the student wasn't sure, so I asked them to tell me the first step, which I wrote down in the Your Turn box (Your Turn 5), and they finished the explanation by themselves without further prompting. I then sent students to my big whiteboards that I have around my room to work in pairs answering the following set of questions from the textbook. After a few minutes, they had all made really good progress (much better than when I have them work at their desks). During this time I had been able to quickly see the work of every student as they were all on display to the whole class. This was followed by another quickfire round of example problem pairs, where there were factors in brackets. I made a big deal to refer to them as factors throughout. Then back on the whiteboards for some more practice. I followed this same pattern through simplifying algebraic fractions that needed to be factorised first, and here is where my over emphasis on the need for factors paid off. Another set of example problem pairs on linear expressions, with time on the boards, and then quadratic expressions. Students spent 25 minutes working individually in their books on the questions for these, as I explained to them that they were more difficult and they would need to give it their full attention. For a class that are generally quite chatty, they worked pretty much in silence for 20 straight minutes on difficult algebra problems. I was in shock (in a good way!) I did make one error here when addressing prior knowledge. Although I got them to factorise a few quadratics so I could check if they were OK with this, I obviously didn't give them enough time on it, especially those with a coefficient of x2 which was not 1. This ended up distracting from the simplifying fractions, and I decided to ask them to skip a few questions to focus on the skill we were looking at today. I need to come back to reviewing more complicated quadratic expressions, and build in some algebraic fractions too. The following lesson we moved on to multiplying and dividing algebraic fractions, and followed a similar process, though with only 2 example problem pairs (they didn’t need any more by this point). I also started this lesson with a set of questions on multiplying and dividing numeric fractions, and showed the class how to cross cancel before performing the operations (which some had never seen). I then had them work on a challenging exercise from one of the old textbooks recommeded by Jo Morgan at Resourceaholic. I particularly liked question 10, and once we had found the answer, I was even more convinced of the beauty of this expression. I explained to the class why it was beautiful, and challenged them in the last 5 minutes to create their own beautiful expression that simplified down to an integer. I have now got to teach adding and subtracting algebraic fractions, and then dealing with complicated equations with algebraic fractions too. I am going to try to follow a similar process throughout the rest of the unit. I have found the quickfire example problem pairs to be a great way to keep my lesson moving at a good pace, as I have found in the past that these can really slow the lesson down. Although sometimes that extra time is really needed to dig deep into the example and details, in this case, I think seeing lots of different examples close to each other allowed my students to make connections for themselves. All students were able to perform in the lesson, fully able to deal with all the stuff we have covered so far. I am happy that I have laid a groundwork of success for the students before we now move into the slightly more tricky bits of the unit. Hopefully that feeling of success will run through, and students will continue to believe they can do it. I know that them performing in the lesson is not a good indicator of their long term learning (these will be cropping up in starters and quizzes over the next few weeks and months to guarantee that), but I have never taught algebraic fractions before when all students left the room able to do it (except when I have taught the top set Additional Maths class). And this is definitely a good step in the right direction. After each of the lessons in this sequence I left the class feeling like ALL my students knew more than when they entered my classroom. On top of this, ALL the students were working for the full 40 minute period, fully engaged by both the quick pace of the example problem pairs and the use of the whiteboards for answering questions. Overall, this is definitely something I am going to build into my teaching on a more regular basis.
3 Comments
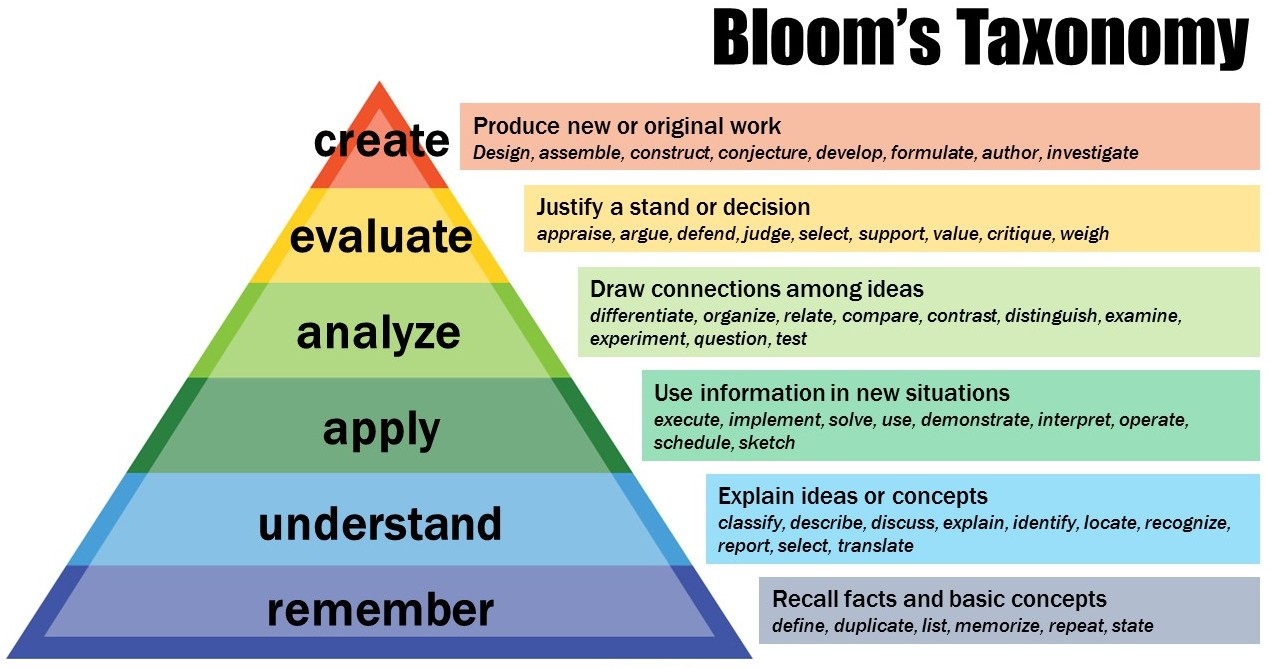
Bloom's Taxonomy and the pyramid shown above are commonly known in educational settings. The hierarchy was designed to help educators push students to higher level thinking, and was intended to help with the development of cognitive abilities. However, I feel that it is often misinterpreted in educational settings. Many people are under the impression that Bloom's Taxonomy says we should always be aiming for the top three tiers of the pyramid. These are the higher order thinking skills we want our students to develop, so these are the ones we should be practising regularly. On the other hand, there are people who see the pyramid and immediately cast it aside, having sat through training sessions stating the above, or just having it hammered at them so often they have grown tired of it. These people argue there is no use in it as it is old (1956) or not based on a thorough research base, which is now significantly more advanced. But I feel both camps are on the wrong track here. As far as I know, Bloom never intended to suggest that we must always aim for the top, and it is this that causes the problems (on both sides). I actually like the Pyramid structure of the taxonomy, as to me it makes things very clear. To achieve understanding, you need a firm foundation of knowledge. To be able to apply your knowledge successfully, you need to understand it. You cannot analyze something if you cannot apply the basic ideas. To evaluate (that is justify your conclusions) you need to first analyse the material. And, finally, to be able to be creative in a domain, you have to be able to justify your opinions first. This is the nature of a hierarchy: they build upon themselves. You have to climb to the top, and it is not possible to jump straight there without doing the ground work. This fits in with my view of creativity as the pinnacle of expertise within a domain. We can only be truly creative when we know a lot about something. As an Art teacher once told me, "You have to know the rules in order to break them" when referring to the work of Pablo Picasso. But there is another aspect of the pyramid image that I like. Notice the size of the pieces. They are not equal. This has two implications:
I want to clarify for the second point I mean throughout school. When students arrive in our class they already have a vast amount of knowledge they have learned (both in and out of school), especially if we teach in secondary education. That means that most of that block may already have been learned, and we can move up more quickly. In general, the further through their studies of a particular subject, the more higher level thinking we should require. However, it is dangerous to assume this is the case. If there is missing knowledge, or even misconceptions, then the other aspects of higher order thinking will be built on a shaky foundation, and, inevitably, will lead to poor performance and less learning. One of our roles as a teacher is to check for understanding and knowledge before moving on to the higher levels of Bloom's Taxonomy. And for those people who sit in the latter of the two camps described at the start? Well, I think this interpretation fits in well with ideas from modern cognitive science. For example, Daniel Willingham talks about How Knowledge Helps, which is saying that the bottom of the hierarchy is really important. I think that there is a lot of benefit to the ideas of Bloom's Taxonomy, but, as with many things in education, when it is misinterpreted it can be killed off. Further Reading on Bloom's Taxonomy
Here are three posts from some of the big hitters in education with their take on the Taxonomy. https://learningspy.co.uk/featured/didaus-taxonomy/ https://theeconomyofmeaning.com/2017/08/24/a-longer-piece-on-the-taxonomy-of-bloom/ http://teachlikeachampion.com/blog/blooms-taxonomy-pyramid-problem/ New School Year We have just started our new school year in Peru, and the kids have been back for a week, after an INSET and Preparation week. It has been tough to get back into the routine, but it doesn't take long to get back in the habit. In the INSET week I launched our new Principles of Great Teaching document with two sessions with our staff: introducing the document in general and then focusing on the first standard, which is having an activity for students to do as they enter the classroom (inspired by Doug Lemov's Do Now). It has been accepted well by colleagues, who have commented on it being useful to track their own development, and as a guide towards great teaching. Most people were even on board with the Do Now, though we will have to see how that goes as term progresses. In general, people were very positive about the whole week, and I have had a couple of comments about it being more useful this year than usual, even though staff had less time to prepare for their classes. My personal focuses for this year that are taken from the Principles are:
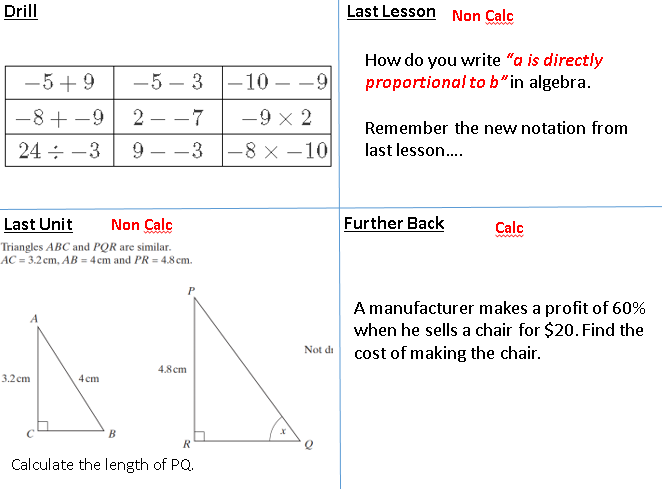
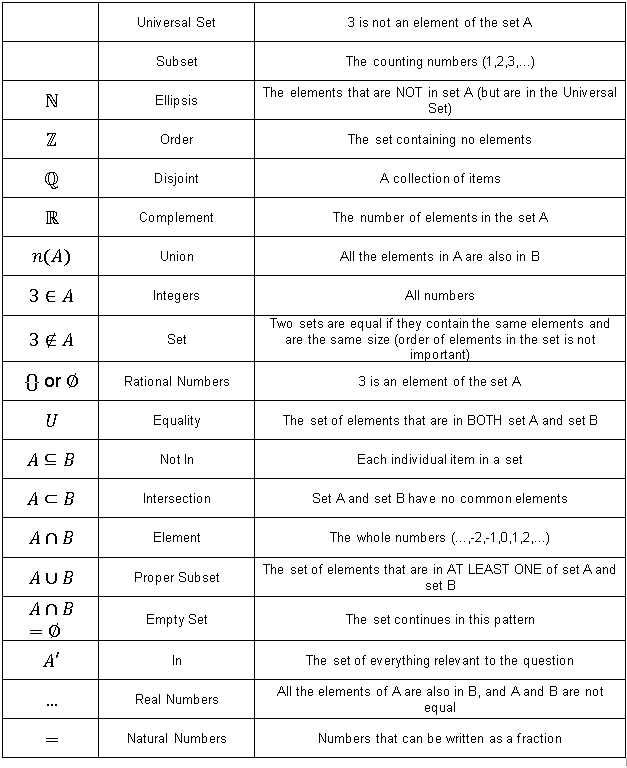
In terms of teaching, I have started my classes with more clarity on my expectations for lessons with me, by producing this document which I have on my walls, and have given copies to my students. Introducing Direct Variation with S4 In the first lesson of the year I introduced my S4 class (taking IGCSE this year) to the concept of two variables being connected by a constant factor, and linked this to previous work on proportion. I ended by showing them the notation for a is directly proportional to b. We continued this work in the double on Tuesday. I started with the traditional Last Lesson, Last Unit, Further Back, but I have added a new section this year: Drill. The idea is to drill some of the most basic skills so they do not occupy space in working memory when solving more complex problems. After reviewing a couple of bits from this, I moved on to a silent example problem pair. I used Show Call on the Your Turn problem, choosing a couple of pieces of work I noticed while circulating, one using 0.75 and the other using 3/4. Previously I have written the examples on the SMART board, but this year I have decided to do it using the visualiser live on a copy of the booklet I give to students. This worked well as it gave them more guidance on how to lay it out (although I needed more space to keep the vertical structure I would have preferred). I then had students complete a short exercise in pairs on the big whiteboards I have around my room. I much prefer this way of working than using mini-whiteboards, as it is easy for me to see everybody's work, and to draw attention to important points. For example, one pair started with x=ky whereas everybody else started with y=kx. I used this to identify that their values of k were different, but the final answer would be the same. As it was on a big board, it was easy for everybody to see. After a couple of groups had finished the 10 questions, we moved on, and I had the class generate the 5 steps for the process. I insisted on them using proper vocabulary (substitute not "put in"). I followed this with a quick Pepper round (also Lemov), asking them quickfire questions on their squares, cubes and roots. This energised the room nicely before seguing into some more examples-problem pairs, where we have proportional to squares and roots. I actually decided to have students attempt Example 4 by themselves before I showed them, and several got stuck by the fact that it was asking for the value of the subject of the formula. When I then showed them, they had had a chance to think about it, and this step made more sense. Then I used a few Diagnostic Questions to check for understanding of notation and steps. We finished with some independent practice questions taken from Dr Frost. Next lesson we move on to Inverse Proportion. Gratitude I downloaded the 5 Minute Journal App towards the end of the holidays to start developing my own reflective processes. Each day I have to come up with 3 things I am grateful for, 3 things I will do to make the day amazing, and then in the evening reflect on 3 things that were amazing, and 1 thing I could have done to make it even better. I am finding it difficult to come up with new gratitudes each day, but it is slowly becoming easier. I have built it into my morning and evening routine now, so I am remembering to do it. I am starting to feel generally more positive about situations, and I am hoping that this will help me become more charitable in my interpretations of what people say, as well as making me more aware of my own good fortunes. It is very easy to focus on the negatives, and this will hopefully stop me from doing that so much. Team Teaching My colleague and I who are both teaching IB Mathematical Studies, have decided to combine our classes and team teach this year. It is the second year of the course, and we always have a few students leave school at this point (it is only compulsory until 17 in Peru), so we both have small classes (less than 10). We figured this will allow us to provide more support, especially during independent practice. We are going to see how it goes, and I will reflect more on it as we progress, but I am excited to give this a go. Sets Notation Matching We started the new year with a unit on Sets and Probability with the final year IB Mathematical Studies classes. Sets is something they have encountered several times before, and it is on the IGCSE that we do. However, the notation is always something that causes confusion. To start the unit we decided to do a matching activity with the symbols, the names and a brief description. The activity was done in pairs, and there was lots of good discussion and questions about some of the notation and words. They had not seen the words Order, Disjoint or Ellipsis before, so these threw a lot of them, even though they had an idea of what the symbols meant. This gave us a pretty good idea of which were the problem areas (subset vs proper subset).
|
Dan Rodriguez-Clark
I am a maths teacher looking to share good ideas for use in the classroom, with a current interest in integrating educational research into my practice. Categories
All
Archives
August 2021
|
|
Indices and Activities
|
Sister Sites
|
©2012-2023 Daniel Rodriguez-Clark
All rights reserved |
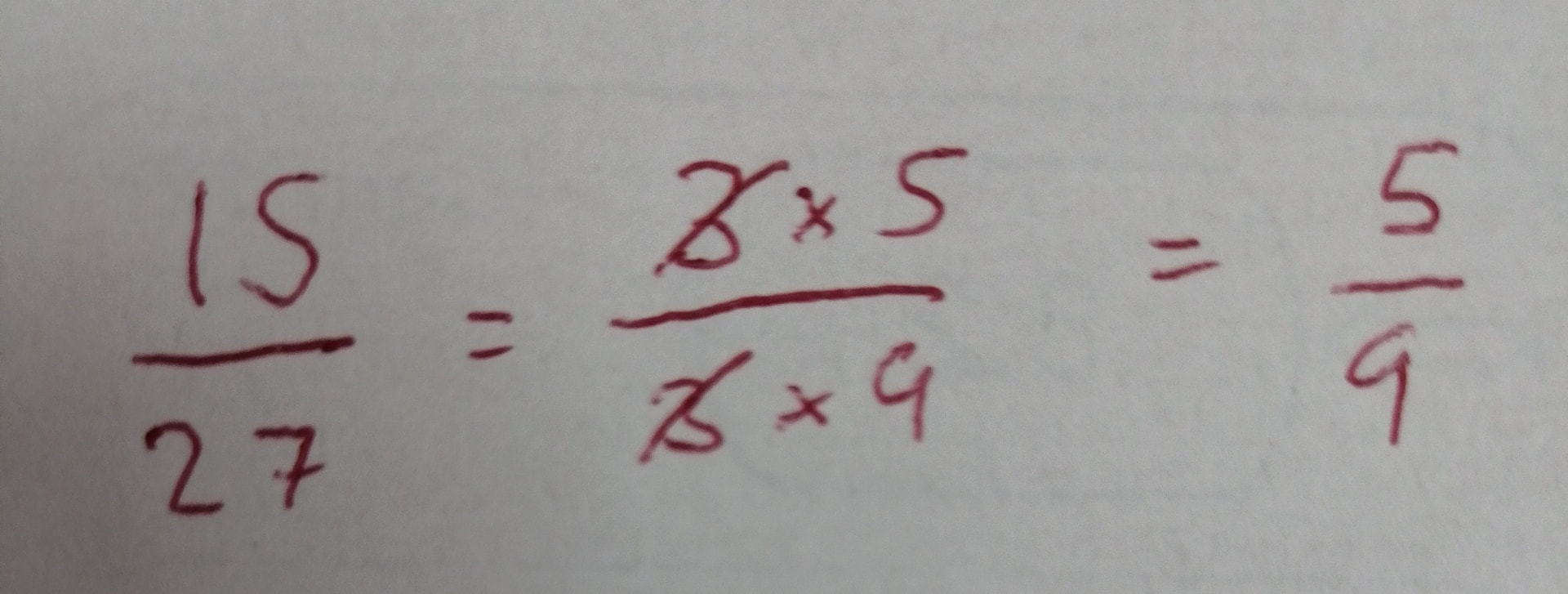

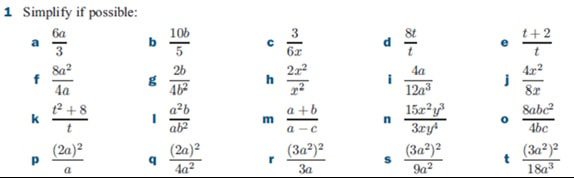

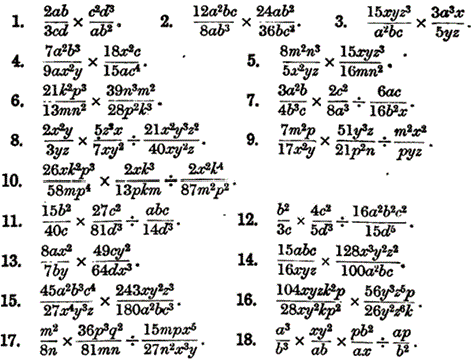





 RSS Feed
RSS Feed
