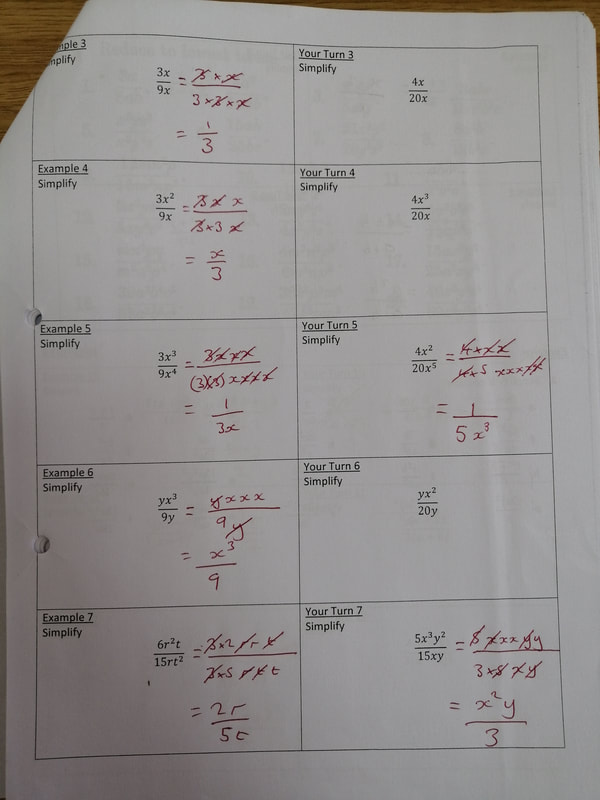
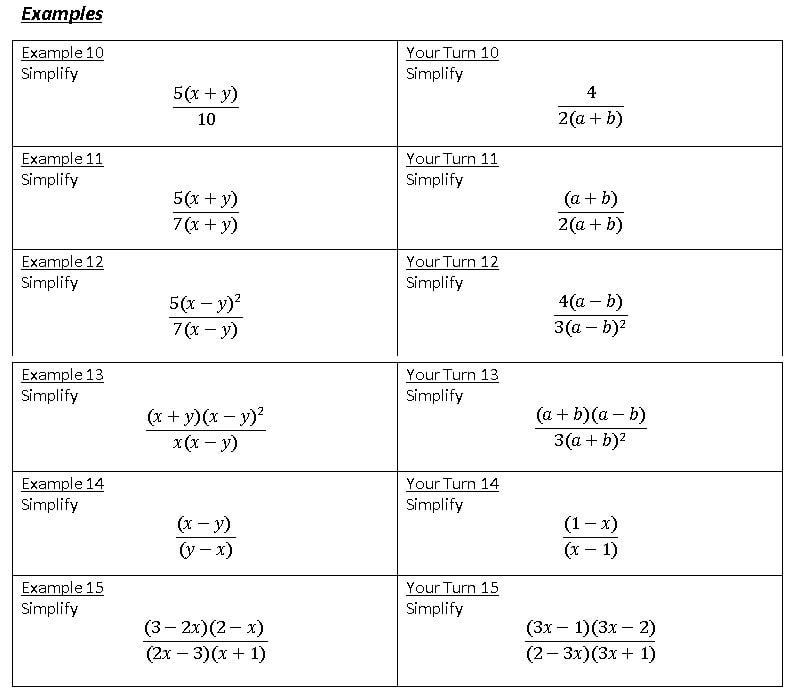
I have been teaching algebraic fractions to my S4 IGCSE class. I am about halfway through the unit, and I wanted to take some time to reflect on how it was going so far.
I started the unit by getting students to answer a serious of questions on cancelling fractions and equivalent fractions. I generated these using my website as I wasn't concerned about the order of questions as it was all stuff they had done before. However, in reviewing this, I decided to talk explicitly about what we are doing when simplifying a fraction. I was very deliberate with my wording "We are looking for common factors in the numerator and denominator that we can cancel". In saying this I broke the numerator and denominator into a product of factors, as shown below.
We then extended this, with me saying "To simplify algebraic fractions we find common factors in the numerator and denominator which we can cancel."
Following this I ran through a series of Example Problem Pairs (shown below). I have started doing this using my visualiser so students can see the layout I use in the booklet they have to copy the examples into. I broke up the numerators and denominators into the factors, then cancelled them (I have always taught spotting these before). There are 9 example problem pairs, showing different types of simplifications they may come across. As this was quite a lot of examples, I didn't want to spend ages going through them all, so I decided to do it quickly.
For each example, I called students attention to the board ("Eyes on the board" - I have been working with them for 6 months on how to behave during examples, so this is all that is needed most times), and then I worked the example on my copy of the booklet. They are watching the screen, not talking and not writing. In this case I did not feel the need to narrate after doing the example. As soon as I was finished I said "Your Turn", and all students copied down the example and attempted the corresponding problem. I then Cold Called a student to give the answer to the Your Turn, making an effort to congratulate them for getting it right. In one instance the student wasn't sure, so I asked them to tell me the first step, which I wrote down in the Your Turn box (Your Turn 5), and they finished the explanation by themselves without further prompting.
I then sent students to my big whiteboards that I have around my room to work in pairs answering the following set of questions from the textbook. After a few minutes, they had all made really good progress (much better than when I have them work at their desks). During this time I had been able to quickly see the work of every student as they were all on display to the whole class.
This was followed by another quickfire round of example problem pairs, where there were factors in brackets. I made a big deal to refer to them as factors throughout.
Then back on the whiteboards for some more practice.
I followed this same pattern through simplifying algebraic fractions that needed to be factorised first, and here is where my over emphasis on the need for factors paid off. Another set of example problem pairs on linear expressions, with time on the boards, and then quadratic expressions. Students spent 25 minutes working individually in their books on the questions for these, as I explained to them that they were more difficult and they would need to give it their full attention. For a class that are generally quite chatty, they worked pretty much in silence for 20 straight minutes on difficult algebra problems. I was in shock (in a good way!)
I did make one error here when addressing prior knowledge. Although I got them to factorise a few quadratics so I could check if they were OK with this, I obviously didn't give them enough time on it, especially those with a coefficient of x2 which was not 1. This ended up distracting from the simplifying fractions, and I decided to ask them to skip a few questions to focus on the skill we were looking at today. I need to come back to reviewing more complicated quadratic expressions, and build in some algebraic fractions too.
The following lesson we moved on to multiplying and dividing algebraic fractions, and followed a similar process, though with only 2 example problem pairs (they didn’t need any more by this point). I also started this lesson with a set of questions on multiplying and dividing numeric fractions, and showed the class how to cross cancel before performing the operations (which some had never seen).
I then had them work on a challenging exercise from one of the old textbooks recommeded by Jo Morgan at Resourceaholic.
I particularly liked question 10, and once we had found the answer, I was even more convinced of the beauty of this expression. I explained to the class why it was beautiful, and challenged them in the last 5 minutes to create their own beautiful expression that simplified down to an integer.
I have now got to teach adding and subtracting algebraic fractions, and then dealing with complicated equations with algebraic fractions too. I am going to try to follow a similar process throughout the rest of the unit.
I have found the quickfire example problem pairs to be a great way to keep my lesson moving at a good pace, as I have found in the past that these can really slow the lesson down. Although sometimes that extra time is really needed to dig deep into the example and details, in this case, I think seeing lots of different examples close to each other allowed my students to make connections for themselves.
All students were able to perform in the lesson, fully able to deal with all the stuff we have covered so far. I am happy that I have laid a groundwork of success for the students before we now move into the slightly more tricky bits of the unit. Hopefully that feeling of success will run through, and students will continue to believe they can do it.
I know that them performing in the lesson is not a good indicator of their long term learning (these will be cropping up in starters and quizzes over the next few weeks and months to guarantee that), but I have never taught algebraic fractions before when all students left the room able to do it (except when I have taught the top set Additional Maths class). And this is definitely a good step in the right direction. After each of the lessons in this sequence I left the class feeling like ALL my students knew more than when they entered my classroom. On top of this, ALL the students were working for the full 40 minute period, fully engaged by both the quick pace of the example problem pairs and the use of the whiteboards for answering questions.
Overall, this is definitely something I am going to build into my teaching on a more regular basis.
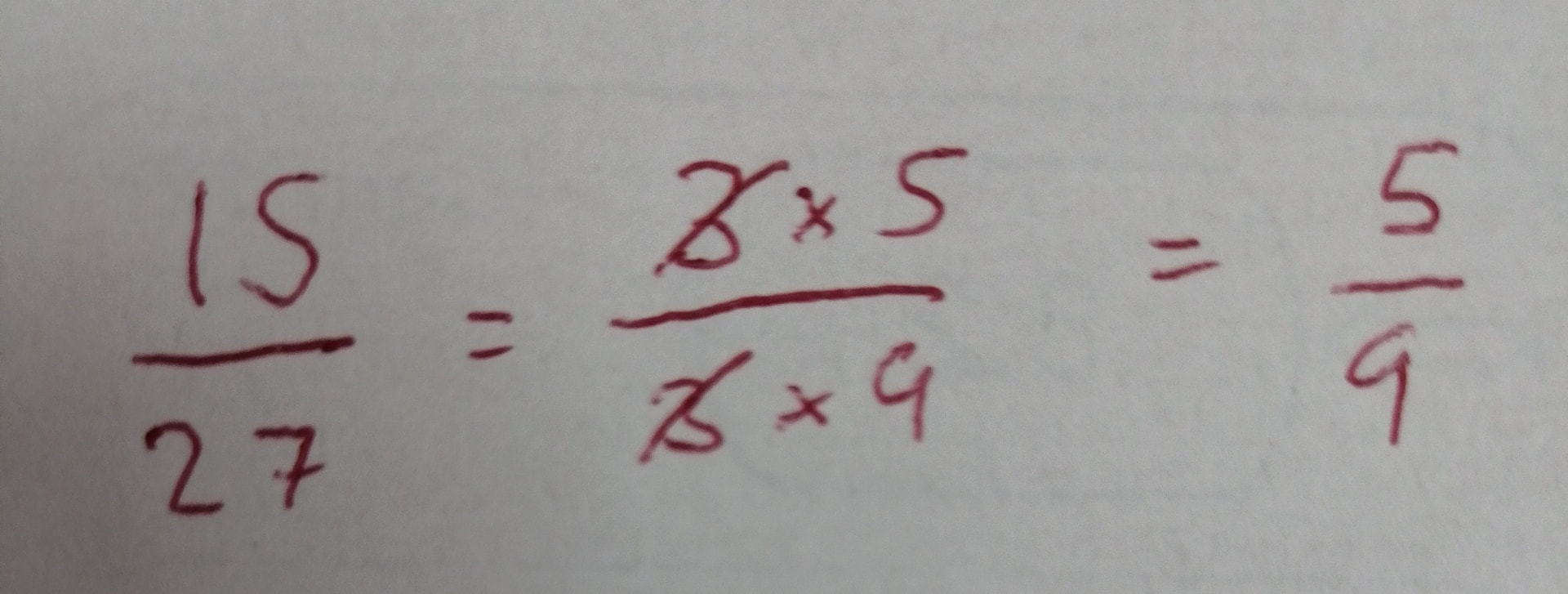
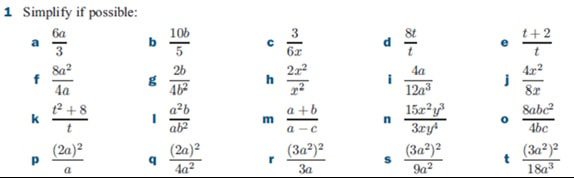
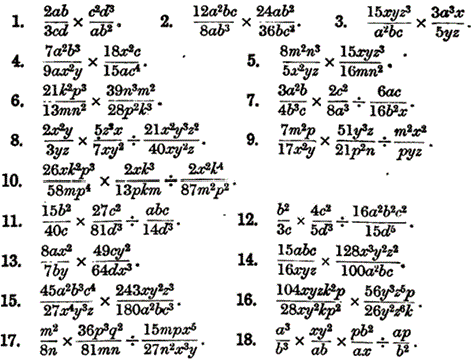
RSS Feed
