|
In a recent lesson with my IB Maths AA SL class, I set them this indices question to simplify as part of the starter activity. They struggled. A lot. Since teaching via Zoom, I don't usually go through these retrieval based activities in class straight away, rather opting to take in their work to check through all their work, which gives me a better idea of what they can and cannot do (in a classroom it is different as I can see their work live). Very few of them got anywhere near close to solving the problem. In the following lesson, they asked me to go through it, so I did. After showing them how to do it, I made a passing comment about enjoying doing this kind of problem, even finding it relaxing. Even via Zoom, I could tell the reaction of my students. Some of them even turned their cameras on to show their disbelief. How could I enjoy solving this kind of problem? How was it even remotely relaxing? This provoked a rather interesting discussion where we talked about the things we find enjoyable. My point was that when you can do something, but it requires a bit of work, that is normally what we find fun. That is, learning is fun if you know enough to be able to learn. We discussed how some people enjoy music or sports, and the reason why is normally they are relatively good at it. And then they enjoy getting better and doing more difficult aspects of that course. It is the same with Maths (and anything else really). If you are constantly failing at it, you will not enjoy it. But if you can do it, with a bit of effort, normally you will enjoy it. They could understand this point. I don't think they had ever really thought about why they enjoy some things and not others, and it helped them see how I could enjoy solving a Maths problem. I told them that my job was to help them know enough that they could enjoy solving Maths problems. Now I just need to live up to that!
2 Comments
Our students are currently heading towards their mock examinations, and usually at this time of year I do an assembly with them to talk about effective revision. But this year we are all on lockdown due to COVID-19, and it seems unlikely that we will be back in school any time soon. So I decided to do something I have meant to do for quite some time: put together a brief guides for students and parents on how to revise effectively. I wanted to build in the elements that I usually present, which are all evidence informed, and present it in a way that would help students identify both why it is important and what they should actually be doing. I have seen other similar ideas before (a couple are linked in the Further Reading section), and there is nothing groundbreaking in what is included. Mine is just another example that people might find useful to share with their students, parents and colleagues.
I am writing this as we are in the middle of the global Covid-19 pandemic. This has shut schools across the globe, leaving most children to be taught remotely. I have blogged before about how I have used Online Live Teaching in this situation. But one of the things that seems to be on everybody's mind is how do we get students to engage in this type of teaching. Without having students in the class it is much more difficult to judge engagement, and for some it is even difficult to ensure they are present and doing the work. This raises the debate over what we actually mean when we talk about engaging students. As a younger teacher, I firmly fell into the camp of believing that lessons should be fun in order to motivate students to be engaged in lessons. I would spend hours designing activities, be it card sorts, bingos or jigsaw activities to keep the students busy and active throughout the lesson. My thinking behind this was that if they were kept busy, then they would be engaged in the lesson. Well, if I am being honest, I do not really mean "my thinking" in that last sentence. I mean "I was told/led to believe". Not necessarily directly, but certainly through the types of activities we were shown in my teacher training. These were the activities that were modelled to us, and so these were the types of activities that we employed in our teaching. And it was all about that holy grail of education: student engagement. For those first few years of my career my job was to engage the students in the lesson, usually by making it fun in some way. Perhaps that was through the way I "performed", or through the activities I prepared. But my main concern was that students enjoyed lessons. But now I see things differently. I still believe in engagement. We know from plenty of research that it is vital that students are engaged with the learning in order to learn the material (for example, check out MARGE by Shimamura). But there is a subtle but important difference in the language. You may not have noticed it. At the start of this post I referred to students being engaged in the lesson. Now I am saying that students are engaged with the learning. And that is the crux of the issue when it comes to discussing engagement. Is our job to create engaging (fun) lessons? Or is it to make the content that students need to learn engaging? These are very different things. You could argue that the former is easier (though the workload was killer!) in that it requires far less thought on everybody's part. But again, that is the problem. As Willingham says, "memory is the residue of thought", and if we want students to remember things, we have to get them to think deeply about those things. And interestingly, this normally piques their interest and gets them engaged in the lesson. So in this time of remote teaching when we are all concerned about keeping students engaged in their school work, think about this: do you want students to have fun, or do you want them to learn something? If it is the latter, perhaps you would be better off thinking hard about the content you want them to know, and, more importantly, how you can get the students to think really hard about it. Engage them in the learning, and they will be engaged in the lesson.
There has been plenty of debate on twitter the last few days over the effectiveness of teaching live online lessons vs setting work for students to complete in their own time. In other words, whether we should be teaching in a syncronous or asynchronous way in the current school closures. Mark Enser goes into detail of why he thinks the asynchronous model is a better approach here as a response to some rather antagonistic tweets from a former Schools Minister. Enser accepts that different circumstances will mean that each model will be more effective in different situations. At the end of the post he asks for anyone who has been teaching live online lessons to share how they have made it successful, so that is my plan for this post. My situation First I want to state that I know that what I am doing would not work for everybody. Even those in a similar school situation have different home lives. I am not sharing this to say others should follow my lead, but rather that here are some things that have worked for me. At the start of the lockdown I posted a blog with 5 tips. I stand by those now, though there are certainly things I might add! As I write this we have been doing online teaching for 7.5 weeks since the schools were closed here in Peru. This started 1.5 weeks into our new school year. We are currently on a week's break before starting the second term of 9 weeks which will be done online too. It is very possible we do not return to school premises until 2021. I mention this to make it clear that we are in this position for the long term, and so suggestions of just reviewing and mastering content students have already studied are not appropriate for us. I work in a private school. This brings two things into the mix. Firstly, our students largely have their own devices (year 9 upwards all have laptops in school normally, and years 7 and 8 use them in certain lessons, so most also have their own) and Internet connections are not an issue (well, no more than are usually an issue here). Secondly, our salaries are dependent on parents continuing to pay the fees, and so there has to be a large element of 'pleasing the customer' at this time (more so than usual). In terms of my technology I have a work laptop which I am using for the Zoom call, and then have my personal laptop set up beside this so I can do registers, see classkick progress, view the worksheet without having to jump between tabs on the work laptop. This has been an incredibly important part of my work flow solution. Working at a private international school also has an impact on the number of periods we teach. We have 40 minute lessons and there are 40 periods a week. The maximum teaching load is 28, and most do not have more than 25/26. I also have a post of responsibility so have a lighter timetable. I have a two and a half year old at home. He has not been able to leave the house for 7 weeks and is going stir crazy because of it. But fortunately my wife stopped working when he was born, and so she is taking the brunt of looking after him. Of course, he doesn't completely understand and finds it hard for me to be at home and not be able to see me, and this does lead to some interruptions. But my school have been incredibly understanding of home situations from the outset. We are sticking to the normal timetable, and the only requirements on staff have been that they must have at least one live sessions with each class each week, and they should be available during timetabled class periods, but this can be via email/Google Classroom. So given that many of the practical problems with live teaching are not an issue for me, I have decided (as have our whole Mathematics department) to teach all lessons live through Zoom. What I am doing This year I am teaching two year 7 classes, a year 12 IB standard level class and a year 13 IB Higher Level class. I have taken a different approach with the different age groups, but I do a Zoom lesson every period. With the IB classes I have broadly followed what I do in school normally. As we are working towards and external qualification, there is an element of needing to cover the content, and this is taking a little longer than it normally would. I have cut the retrieval starters down for this reason, doing one question in single periods, and then following the Spacing Concepts I started this year in the double period. In terms of the rest of the lesson, I am still using the lesson sheets I produce for IB classes. Students either print these or have them open of their screens and write in an exercise book if they have no printer. I do not have a printer at home, so I am writing in an exercise book. I use my visualiser and screen share with the class my book, and work through examples as I do in class. Sometimes I will bring out a mini whiteboard under the visualiser to answer tangentially questions. Then students do a your turn. Where in class I can wander around to see their work, in Zoom I am making more use of cold calling students to talk through their entire solution, and asking if anybody did it differently. For shorter questions I get them all to type their answer in the chat function on Zoom, which I have set so that only I see their responses. I am more reliant on them asking for help than I would like, but it seems to have worked well, as the quieter students are asking through the chat. After some input, they generally work on some independent practice. I am making use of Classkick (I made this guide for our staff) and Desmos activities which both allow me to see student responses, but mainly for IB they have questions to do from the textbook, which have answers they can check. One of the mistakes I made early on was not ensuring they knew where the answers were, but now they are in the habit of checking themselves. Keeping them on the Zoom call but muted has become the norm here. This was a request from the students who said they were too easily distracted working in their rooms without it. This also enables them to ask questions if they get stuck, and sometimes I will put them in a Breakout Room to discuss it with somebody else from the class. With my year 7 classes I am taking a different approach. I am uploading a presentation to Classkick, and producing an assignment in Classkick for each lesson (labelled week 7 lesson 3 etc). The first slide is the starter activity which is Numeracy Ninjas. I have found this more important for the younger students as they arrive to the Zoom call in dribs and drabs, and this gives them something to do straight away. One benefit of Classkick is that I set it to mark automatically after 5 minutes. After this I will usually introduce the idea for today's lesson through an example. I have mostly been doing this by editing the Classkick assignment live. If they are on the page they see my edits appear immediately. I then talk through these on the Zoom call. Whilst doing this I lock the assignment in Classkick so they cannot edit it. Then they do some practice. This will probably involve some your turns first which I check before they can move on to the main exercise (in Classkick they can call me to check their work). The main exercise is from the White Rose Maths resources (we changed our scheme of work to theirs this year), and I have set it to self mark where possible. I then keep a view of the whole classes work and can see their work live. I will check questions that can't be self checked (written answers) and answer questions which they can ask through Zoom or Classkick. Some concluding thoughts Some of the benefits of doing lessons live have been:
As I said at the start, I am not saying anybody else should go down this route, and I accept that the practical limitations could get in the way of this being a reality for many teachers. But I have found a way to make it work for me, and I feel like I am able to meet the learning objectives for the students this way in a more effective way than through an asynchronous model. The biggest problem with online teaching (in either model) is checking for student understanding at the time of input. Through Classkick, questions and answers through Zoom chat and cold calling explanations of answers I think I have managed to make a good stab at being able to do this fairly effectively. I would love to hear how other teachers are managing this type of teaching? What were the problems and how did you overcome them? What are your top tips?
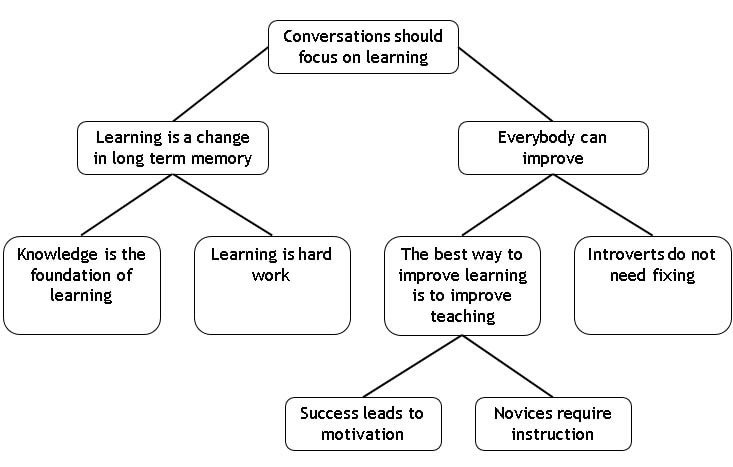
In Better Conversations, Jim Knight briefly talks about the power of assumptions. We all have different core beliefs and assumptions, and often disagreements that we have are based on differing assumptions that we hold. This is true in all aspects of life, including our views on education. The problem with assumptions is that we tend to defend them aggressively when we feel they are being attacked. By sharing our underlying assumptions we can help each other see why we disagree, which should help conversations be more constructive. If we do not know the assumptions our conversation partner holds, then we are liable to think they are stupid for what they are saying, as we are judging their comments against our own assumptions. These assumptions (or beliefs, values, opinions) feed into everything we say and do, so helping others to understand them will help others to understand our points. Similarly, by finding out the underlying assumptions of others, we are in a better position to understand their points. So, here are some assumptions I hold about education. 1. Conversations should focus on the learning There are a lot of things going on in a school, but the primary purpose is to give students the best learning opportunities that we can. For this reason, conversations we have in schools should focus on the learning of the students as much as possible. By keeping a relentless focus on learning within meetings, we don't waste precious time talking about things that will not affect student learning. Just like Willingham suggests we plan by thinking about what students will be thinking at each stage, when in meetings we should always be thinking about how this will impact student learning. If the answer is "Not Much", then we need to consider if we could be talking about something more impactful. I get frustrated when conversations become focused on details that have little impact on student learning, and I will always try to bring it back to what I think is the most important thing for us to be discussing. Of course, that doesn't mean we should agree on everything about learning, but focusing our discussions on this will give us the biggest chance of having the best impact we can.
Over the last couple of years I have moved to a booklet model of teaching my IGCSE classes. In other posts I will detail how I put together a booklet and how I plan lessons using a booklet. But in this post I want to start by exploring what I mean by a booklet and why I decided to move towards using them, and why I am now won over by their usefulness. I design booklets for each unit. They cover the different skills within a unit, building up to exam style questions. A booklet is designed to contain all the resources I might need whilst teaching that particular topic. That does not mean I will use everything in the booklet, but that I do have a variety of things available to choose from. Depending on the class, I will adjust what I use. So why do I use booklets? Here are some of the reasons I have come to really appreciate them. It forces me to think about the whole unit (or learning episode) The first huge benefit is that it forces me to consider the whole unit when planning, not just focusing on lessons. There has been a lot of talk recently about the lesson being the wrong unit of time to plan for, but when our time is split in that way, I find it difficult to not plan in those chunks. Using booklets has helped me break through that barrier. In creating the booklet I have to do it before I start teaching the unit so I can give the complete booklet to students when we start. This means I have to think about all the individual skills that form a part of the unit, and how they connect to each other and build up to the big picture. It means I have to consider not just the order in which I will teach these skills, but how I am going to link them together. Rather than teaching a series of 10 lessons, I now teach the unit. Of course I plan what will go in each lesson, but this is really flexible as we can just pick up from where we finished last lesson. So if we get through it quicker than expected, we can move on, and if it takes a bit longer, there is no need to rush at the end of the lesson. Initial time input but saves time in the long run Putting the booklets together in the first place takes a long time. But now I have a set of booklets on 21 units covering the IGCSE, and I can reuse them again and again. In reality, I make adjustments each year, but the bulk of the work is done. In future I can plan a whole unit in about an hour as I just need to review the notes I made the last time I taught it, and make the necessary changes. I can plan for interleaving and Retrieval of linked prior knowledge more easily When planning lesson to lesson I always found that my focus was on the current bit of new learning, and rarely did I think about interleaving other topics in. But with a bigger picture of planning, I can add more interleaved exercises within the booklet. I don't currently do this, but you could also pre-plan retrieval of prior topics within the booklets. You could design an optimal spacing schedule and plan in these retrieval opportunities within other units. No running for last minute photocopies As everything is in the booklet and the booklet is printed for the start of the unit, there is no need to be running trying to get the worksheet copied just before the lesson. It is also cheaper on photocopying as I am not copying things that I end up not using, and there is little wasted white space within the booklet. Three separate worksheets might fit on a single double sided page, instead of 3 single sided sheets. Changed focus on lesson planning from finding activities to thinking about explanations, what I will use, how I can supplement In the run up to a particular skill, I no longer have to spend time finding/putting together a lesson/activity to use. I can focus my attention on thinking about how I will explain difficult concepts clearly, what visualisations I could use to enhance my explanations, and any other materials that might enhance the teaching of that particular skill. I don't forget any skills Perhaps not groundbreaking, but I can't forget to teach something. It is all there and in my face. I can't get to the end of the booklet without teaching everything from it. Of course, I could forget to include something in the booklet, though that is less likely. What does happen is that I realise I need to break a skill into more smaller bits, but I can just take a note in my copy of the booklet to refer to later. Constantly improving And on that note, whilst teaching I can easily annotate my copy of the booklet. This means I can note anything that doesn't work, or works particularly well, as a reminder for next year. As some of my colleagues are also using the booklets, my hope is that they will start making suggestions too and the booklets will continue to improve each time they are used. No need to reinvent the wheel each year. And because I don't need to focus on creating the whole thing each year, I can give my attention to finding/creating more interesting problems. This year, for example, I have tried to put more Open Middle and Maths Venns problems into the booklets. Everything in one place means it is more efficient to navigate to content in lessons - means I can be more responsive in my teaching With everything in the booklet it is easy to navigate as I just say the page number they need to turn to. No getting out different books, or finding the ebook. For most things they don't even need their exercise book as they can write straight in the booklet. This saves maybe 3-5 minutes every lesson, which over a few weeks really adds up. The other advantage to having everything in one place is that I can be more responsive in the way I teach. If students need more practice, there is loads in the booklet so we can just carry on with that. If some students need to be pushed a little harder, there is a challenge question (available for all students, not just the 'high achievers'). If the whole class is ready to move on within a lesson, that's fine, we can just move to the next skill. No filling time as I don't have resources prepared. Standardise the format In Teach Like a Champion 2.0, Doug Lemov discusses the strategy he calls Standardize the Format. The idea is that I can save time and effort checking student work if they all answer in the same format. Booklets are perfect for this as they guarantee that all students will write in the same space. Walking around the classroom you can quickly look to see every response, as they are all in the same space, so you don't need to hunt for them. Students can use them for revision My students have been particularly happy with the booklets in the run up to exams. The booklet gives them a structure to their notes, clearly shows examples, and has plenty of practice questions for them to do. I provide an electronic blank version of the booklet too, so some students use this in their revision, printing it off and filling in the examples and your turns again. What a great way for them to practise the skills they need. So there are 10 reasons I have grown to love the booklet. Many of these relate to workload issues, and many more relate to better teaching. I feel that by using booklets I have been able to focus more on my teaching (explanations, examples, models) and less on the activities. Moving towards using booklets has happened alongside my general switch to a more explicit teaching methodology. I love them. And my students are also overwhelmingly in favour of them. In the next post I will be looking at how I actually go about making a booklet and what I include in them. Do you teach using booklets? If so what are your reasons for using them? If not, have you ever tried it? Is it something you would be willing to try?
This is a story about two teachers: Adam and Zack. Adam believes that students learn best by exploring ideas they are interested in. By linking his lessons to authentic experiences, Adam believes that students will construct their own learning, which will be powerful for them as they are interested in it. Adam motivates his students with challenging real world problems that they want to find solutions to. In Adam's class, students are provided with real choices over their learning, both the content and the skills. Adam wants his students to leave school with the skills to succeed in the future, and is not concerned with the knowledge they have at the end, as content is just a delivery system for the skills. Critical thinking and creativity are the goals of education in the eyes of Adam, and to develop these he gives his students lots of authentic problems to solve. Adam would describe himself as a "guide on the side", facilitating the learning of the students. He sees his job as helping students to develop into their own people, and to be there as a guiding force when students get stuck. Adam's edu-heroes are Rousseau, Piaget, Vygotsky and Sir Ken Robinson. Zack believes that students learn best when they are given clear instruction. Zack uses lots of examples to explain concepts, and he aims to give all his students access to the powerful knowledge that has been developed by generations of humankind. Zack motivates his students by making them successful in the early stages, giving them lots of practice of simple skills which build upon one another. In Zack's classroom, students learn what he has chosen, and he creates lessons to make this as successful as possible. Zack wants his students to leave school with a good understanding of the knowledge that has benefited previous generations: the knowledge he believes to be powerful due to its longevity. After lots of practice on the basic skills, Zack will push students to solve complex problems, believing that critical thinking and creativity are based on the knowledge you already have, and are domain specific. Zack would describe himself as a "sage on the stage", directing students to the content and skills they need to learn. He sees his job as imparting what he knows to his students and ensuring they understand it. Zack's edu-heroes are Engelmann, Willingham, Rosenhine, Bjork and Wiliam. Adam and Zack are about as far from each other as they can be in terms of their beliefs and practices within education. But what's truly important is that they both do everything they do because they believe it is what is best for their students. There is a debate in education as to what the best approach is. And this debate gets very heated. The reason it gets so heated is that we all care deeply about the outcomes of our students. We all want nothing more than to give our students the best start in life, and provide them with an education that will serve them well for the remainder of their lives. But we disagree on how to do that. And, perhaps more importantly, we disagree on what the purpose of education is in the first place. But that's fine. The debate that rages on is what holds us all to account. It is what makes us think about what we do, rather than just ploughing on doing the same as we always have. I was first made aware of this debate when I joined twitter. Before that I was oblivious to the fact that there were large chunks of the education community who thought differently to me. In fact, I wasn't really aware of what I thought. It was only when I started to engage in the debate (mostly from the sidelines) that I began to think deeply about my own beliefs. I went away and read lots of articles and books. Over time my own views shifted because of the debate. But most teachers are not on twitter, and are possibly completely unaware that this debate rages on. They do what they do because that is what they have been told is best. Or that is what they have always done. Or that is how they were taught. But we would never accept an argument from a student that blindly follows one source, without contrasting it to others. So why should we expect teachers to follow one path? Engaging in the debate is the only way to come to terms with who you are as a teacher. Most teachers are not Adams or Zacks, but more like Daves, Tommys or even Michaels. They lie somewhere along the spectrum of the debate. Perhaps they are on one side, but have certain views that align to the other. And this is always shifting. Some people become more extreme in their beliefs. Some sway to the centre. Some completely switch sides. All these changes happen because of interactions within the debate. They happen because teachers are thinking about teaching and education. When I started teaching I was probably a Dave. After discovering cognitive science, I swung to becoming a William. Now I am more like a Rory. Where will I be in two years time? Probably still on Zack's side of the spectrum, but who knows. I didn't expect to be here when I was a Dave! My two takeaways from the story of Adam and Zack are these:
Those who try to shut down the debate, or even win the debate, have probably strayed quite close to Adam or Zack. But their voices are important too. They are the ones who, usually by being provocative in their language, make teachers like me think about my position on certain issues. So next time you find yourself disagreeing with somebody about education, don't dismiss them or try to shout them down. Have a conversation. Try to learn from them. And remember, we all want the best for our students. If you are interested in an excellent post about the different modes of teaching, and how to mix up the worlds of Adam and Zach, check out this post: https://thinkingaboutteaching.blog/2019/08/03/traditional-or-progressive-how-to-get-the-best-of-both-worlds/
|
Dan Rodriguez-Clark
I am a maths teacher looking to share good ideas for use in the classroom, with a current interest in integrating educational research into my practice. Categories
All
Archives
August 2021
|
|
Indices and Activities
|
Sister Sites
|
©2012-2023 Daniel Rodriguez-Clark
All rights reserved |
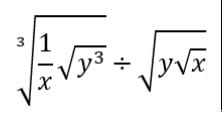







 RSS Feed
RSS Feed
