This activity is one based on something I got told about whilst at Uni. The resource is available for download from TES under Compound Interest in Egypt.

The premise of this activity follows the story of two slaves who helped build the Great Pyramid, and who invested their wage of a sinlge gold piece with a local Money Lender. They were given two options: Simple Interest at 100%; Compound Interest at 1%.

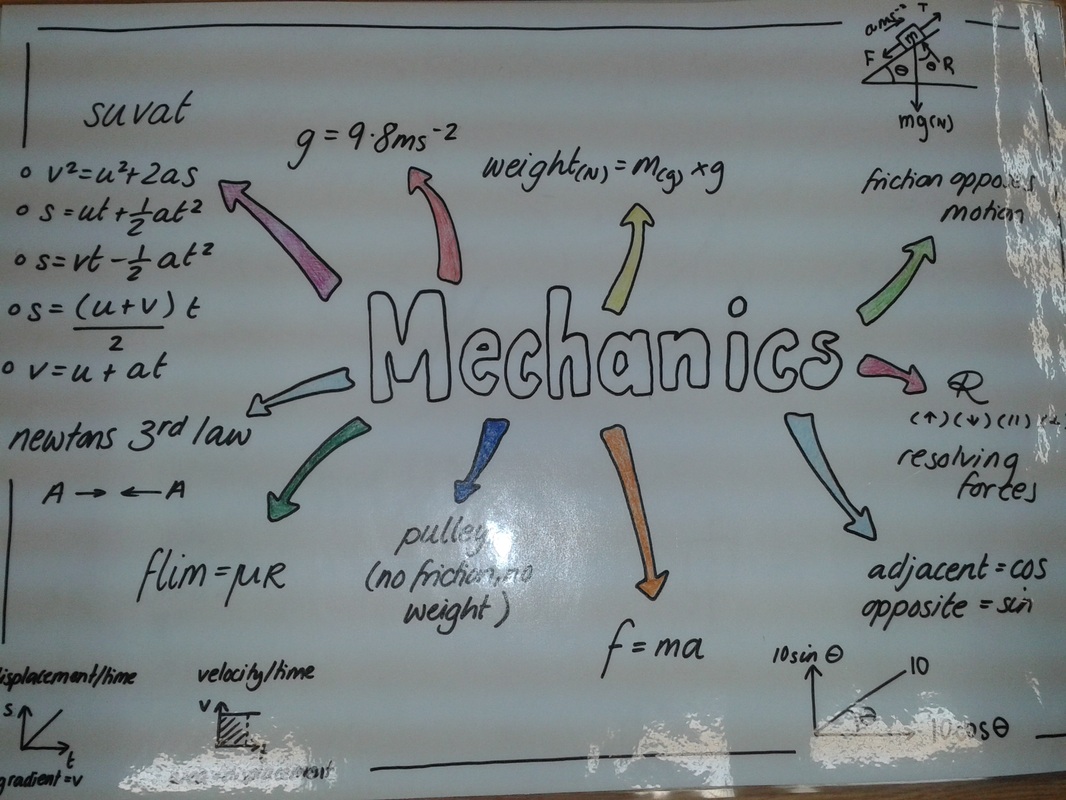
On Fridays I have Year 7 last lesson. I have a top set, and they can generally get on with work, but as everybody, they are pretty tired by the end of the week. I try to plan activities that will get them actively involved in the lesson particularly for this lesson with them.

This week I found this excellent set of rather challenging Area and Perimeter Problems uploaded to TES by JamesBeltrami. His suggestion is to have them printed at the front and have pairs answer questions, and come and collect a new question when done. I took this idea and resource, and changed it slightly.

I have used mind maps many times with my KS3 and KS4 classes to great effect. They are great for getting the kids to spot the connections between different areas of maths, and also an excellent way to review a topic. I am a big fan of them.

It was kind of surprising to me then, when I realised I had never done one with one of my A-Level groups. The opportunity arose just before half term, when my M1 class asked for an overview revision lesson in the last lesson, as they have mocks straight after the break.

QQI stands for QuickQuestion Interface © and is a series of activities I have created for use in the classroom. The basic premise was that I wanted to be able to generate random questions on a variety of topics for students to answer. It started with simple number operations, and has expanded to include areas of shapes, solving equations and many other topics. There is a complete QQI index of all the activities currently live.

I use the activities regularly in my lessons, as starters and plenaries, and they work best when used with Show Me boards. I will put a question on the board, give students some time to answer the question on their boards, and then ask them to put their boards up. I tend to give them a set time, and get them all to put their boards up together, even if they are not finished, so I can quickly see what they have done, and any mistakes I need to address.

Using the students to teach little bits and pieces is something I use fairly regularly in my lessons. It is usually as simple as sitting students in pairs, such that one understands, and another does not quite get it yet, and then the magic happens automatically. Sometimes, I also use those who finish an exercise particularly quickly as an extra pair of hands to help others. This proves particularly useful in topics such as fractions, where some students can do it very quickly, but others still need a lot of support. This provides those struggling with extra support, and those who get it, really have to understand the material to teach it.

In one of my A-Level groups, I have a fairly mixed bag, with some of the students having done Additional Maths alongside the IGCSE we offer, and some having come from other schools for the Sixth Form, with the GCSE. The whole group are very capable mathematicians, but there are large chunks of the C1 and C2 course that those who did Additional Maths have already covered.

In particular, an early problem arose when doing differentiation, since this is on the IGCSE syllabus, so all the students from our school had already done it, but those new to the school had no idea. The major downside to this was that those who had already done it, thought they knew it, and wanted to skim through it. However, as has become apparent recently, they did not get a proper understanding of the First Principles (which is not on the IGCSE), as they felt they knew it, and did not necessarily give it their full attention.

I have been trying different approaches to get round the difference in knowledge, and recently I tried something a bit different.

I used the Area Two starter by Transum with my year 10 group today before we moved on to areas of sectors. The problem asks how many shapes can be made with an area of 2 on the grid shown below, by joining dots with straight lines.

During last term I started to collect a variety of puzzles and problems taken from a variety of places and I have created a "Mr Clark's Box of Puzzles".

There are puzzles taken from a selection of books I have, some classic famous historical aspects of mathematics, some SuDoKu and similar puzzles, and a few puzzles taken from 7puzzleblog.com. When I see a new puzzle or problem, I copy/print it, and laminate it before adding it to the box.

Having the problems laminated not only makes them last a lot longer, but means that students can use whiteboard pens to write on the problems to help them solve them.

The first few times I used the box, I was introducing it to the groups, and I set aside a period of time to actually look at puzzles. We spent 20 minutes or so working on different problems in small groups or individually.

Now, however, the box has evolved into a perfect extension activity for every lesson. Students have puzzles that they have started, and when they finish their work, they can go to the box to pick it up to continue, or to find a new puzzle to start.

The students love it, and many work so much harder so that they can get on to the puzzles. The amount of thinking that goes on with each puzzle is also amazing. I am trying to get them to be as independent as possible with the puzzles (though not all of them have realised this yet). I want them to be able to approach problems and think about them before rushing to me to ask for help. I also don't have the answers for most of them to hand (though they do exist somewhere), which I find works well, as if they do ask for help, I can say that I don't KNOW the answer, but can give them ideas for how to think about it.

It is growing into quite a large collection of puzzles quite quickly, and is something that I use in all my classes, and will be able to use with many more classes. The range of puzzles means there is something there for Year 7 all the way through to A-Level mathematicians.