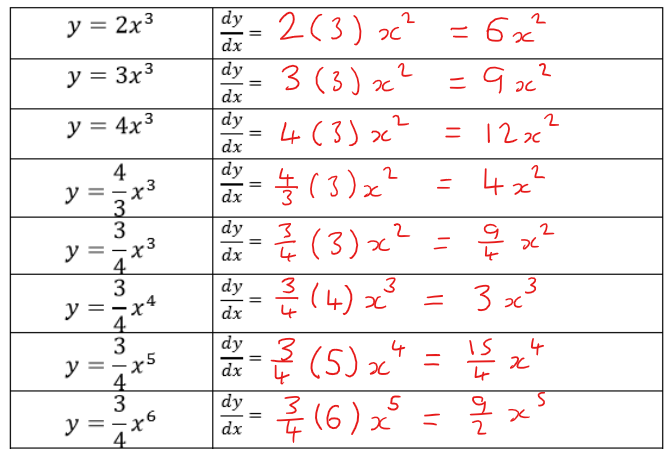
I have previously blogged about some of the activities I use to help students to understand what differentiation tells us (that is what the derivative is), but today I had a great lesson on introducing the actual process of differentiation.
After exploring the idea of the derivative, I explained that differentiation is an algebraic way to find the function, rather than a graphical way.
I started by using a set of examples and asked students to use the Reflect-Expect-Check idea from Craig Barton. I showed them the first couple, then I asked them to reflect on what had changed in the question, expect what the answer would be and then check when I wrote the correct answer. I also made the different parts a lot more explicit than I normally do, as you can see below. The full set of questions is on pages 2 and 3 of this document.
As we went through we stopped at various points, talked about expectations, talked about the "obviousness" of the answer to y=3x (the derivative is the gradient, which is 3) and y=7 (the derivative is the gradient, which is 0) and that these fitted in with the patterns they had already spotted.
One thing I did differently in writing this sequence compared to normal is starting with the general case and showing y=x^2 as a specific case within this.
After this we then did loads of practice, but where I would normally do this via mini-whiteboards in class, since we are remote teaching, I had to find a technological solution. For most things this year, typing in the chat in Zoom has been enough, but I wanted to see the full written derivative from students.
Desmos comes to the rescue. I set up this assignment called My Whiteboards (copied one of the Desmos templates and added a few extra of my own). Then I paced them to the second slide so they were typing Maths. I decided to do this as they need to practice writing in Maths Type before they do their coursework next year. I then projected questions through sharing screen, and students wrote the answer in the desmos, deleting each time to write the next one.
This way I could see their answers as they wrote them, give immediate feedback and see who was participating and who was clearly unsure at any stage.
I used my website to generate the questions, starting at
And ramping up to
Slowly increasing the complexity by adding fractional coefficients, then multiple terms, then negative powers. We ran out of time to get to fractional powers, but will bring those in next lesson.
Overall, all students were successfully differentiating functions like the one shown by the end of the lesson, so I am happy with the progress they made. Unfortunately we only have one more lesson before the end of our school year, so will probably have to review a lot when we go back in March.
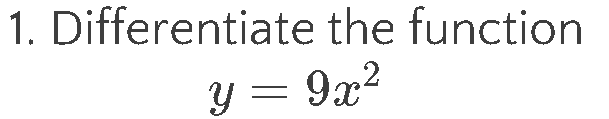
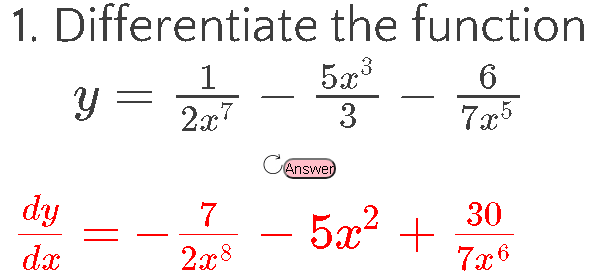
RSS Feed
