I have just finished reading The Teaching Delusion by Bruce Robertson, and it hit all the right notes for me. I found myself nodding along, lapping up what Robertson says, constantly thinking "This is exactly what I think, but said so much more eloquently." In fact, I am thinking of copying a few extracts to give to people when I can't put into words my own thoughts!

I jest, of course. There were plenty of insights in the book that I had not thought about before, and a couple of things I disagreed with.

The main premise is that no matter how good teaching is, it can always be better. This has been a point I have made at the start of each new school year since getting the job of T&L Coordinator, and my most recent phrasing has been "It is both our right and our duty to continue to improve our teaching". I use this wording carefully, to instil the idea that it is our right to want to continue to improve ourselves, get better at our jobs, and become better teachers. This aligns with Robertson's idea of a Professional Learning Culture. On the other hand, we serve a community of children and their parents (who, in my case, pay a fair amount of money for our services), and it is also our duty to them to do the best job we can, which includes continually improving our teaching. Our duty to the parents who pay, yes, but mainly our duty to the young people we have the pleasure of working with, whose future depends so much on what we say and do, how we make them feel, and what they learn from us.

Robertson asserts that The Teaching Delusion is made up of three factors:

1. Most teachers and school leaders think they know what makes great teaching, but they don't;
2. Most teachers and school leaders think they know what it takes to improve teaching, but they don't;
3. Most teachers and school leaders think that teaching in their classroom/department/school is good enough, but it isn't.

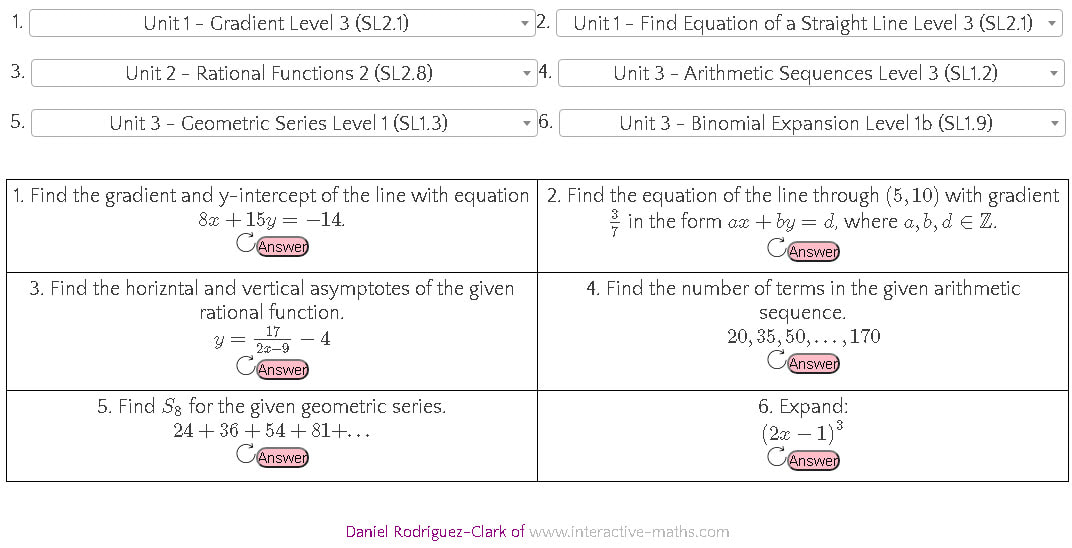
End of a Semester
We are approaching the end of our first semester, and so have a two week holiday coming up. After teaching online since March, with only a week break, I have to say that this is very much welcome. We (teachers and kids) are all tired and having two weeks away from Zoom will be a beautiful thing. We are not allowed to do any travelling as kids under 14 are still quarantined in Peru, so it will be spent at home and going for walks, but I am glad to have some time away from work for a little bit. I have been getting to spend more time with my son as I work from home, which is amazing, but I am looking forward to doing this without nagging feelings in my head about work that needs finishing.

IB Key Skills
I have been using my new IB AA SL Key Skills Generator to create retrieval starters for my lessons. I am using this in conjunction with the Spacing Spreadsheet which tells me which skills to do each week. 

With the lockdown still continuing here in Peru, we switched all classes to double periods, and so I only see the class twice a week, so I do a key skills like the one above on a Monday, and then a shorter definitions/facts recall on Thursday where I simply ask them to define the important words and concepts, and state some important facts.

I have also just finished working on the Binomial Expansion questions, which I am quite proud of. 

​In particular, I went for two different ways for presenting the solutions, based on a conversation on twitter.

Anki
I listened to the recent Mr Barton Podcast with Daisy Christodoulou last week, and one thing that intrigued me was Anki. I had previously downloaded it to my phone as I had heard Ollie Lovell talk about it, and thought it was an easier way to go than the old fashioned flash cards I was using to learn some Spanish, but I never actually got round to setting it up. I will get on this in our two week break that is coming up.

But what really caught my attention was using this with kids. I am thinking about setting up an Anki deck of the key terms and skills that I was recording in the spreadsheet, and then sharing this with kids. They can then do this as the starter, giving them recall practice that is a bit more individualised to what they need. Hopefully this will also get them using Anki to study other things. And then each lesson I can get them to add new stuff to their deck too.

As Craig said at the end in his reflection, it would be great to be able to combine this with randomly generated questions. This is definitely not something I am up to coding myself (mine is largely just a hobby), but it would be interesting. I am thinking a workaround could be to use my IB Key Skills Generator and get students to put a reference to a question in their decks. Then, when it comes up, they go to the site, do that question, and then mark it as right or wrong on Anki as they would a normal flashcard. I think you can even insert a link directly into the card, so that could take them straight to the page.

I will be having a play around with this when we come back in August.

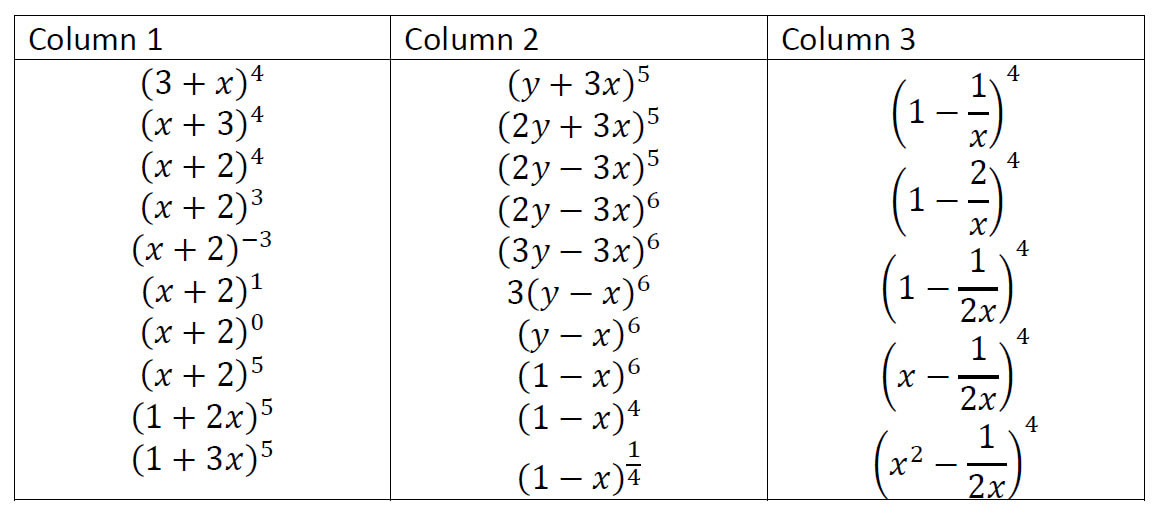
The second book by Craig Barton (well, ignoring the non Maths teaching ones) is everything a sequel should be: it builds upon the greatness of the first, but has its own tale to tell. It gets into the nitty gritty of the story, focusing on one of the smaller parts of the first. And yes, it is a bit controversial.

I am not going to write a summary here. I thought I was, but that would not be able to do any justice to the book. If you are a Maths teacher, you should read the book. Craig is open throughout about not trying to tell you what to do, but rather telling what he does, why he does it, and provoking you to think about how you could adapt those things to work for you (if indeed you find them valuable in the first place). But even if you disagree with everything Craig has to say, then you will still learn a lot from reading the book. If nothing else, if you do all the sequences of questions he provides, you will be giving your subject knowledge a good servicing!

Here I am going to share a few of my main takeaways, and what I want to incorporate into the book.

In my teaching ​

In the very last chapter of the book, Craig gives some advice on "Making it work", and the first thing is to choose one thing you want to try. Well, I am going to ignore him on that! Well, not completely. I am going to choose one thing that is new, and 3 things that I currently do but want to adapt after reading the book.

Reflect, Expect, Check, Explain - this is the new one. I have been using some sequences of questions from Craig's www.variationtheory.com website, as well as making some of my own, but, honestly, they have really just been a set of questions. They have allowed me to direct student attention to certain things, but I have not been systematic enough in my approach to develop their mathematical thinking in the way Craig describes. 

Since starting the book I have been adding some elements, in particular the reflect stage, but I want to make more of this. So I am going to try the full structure, and use the Prompt Questions that Craig suggests (available on his website: http://mrbartonmaths.com/booklinks/). I think I will need to use a template to help them structure the process too. My plan is to try this with my first year IB class, though I need to think carefully about what topic to do this with. We have some recap of indices and logarithms coming up, so that seems like a good fit. I will blog again on this when I give it a go. I have been using some sets of questions with them (such as the one below on Binomial Expansion), and have made short references to the ideas of reflecting on what has changed, but will need to be more explicit about this.

Another aspect that I have not been building in that Is important is the idea of Fluency Practice before the intelligent practice. I used to do too much fluency practice, now I am not doing enough for students to get the most out of these sequences of questions. For students to develop the mathematical skills, they need to be more confident with the method they need to apply first,

Atomisation - this is something I have been exploring, in particular with putting together the IGCSE Booklets and IB Lesson Sheets, but the systematic way Craig approaches it grabbed my attention. Going through the small atoms that make up a new idea and ensuring they are all secure first is something I want to look into further, but think that will definitely need to be a collaborative project. I am also thinking about how I could do some of that in the "flipped" model with IB classes.

Example problem pairs - just a minor adaption to my current process, but I need to find a consistent way to get all their attention on the example. I print examples and your turns in the booklet/lesson sheet, so the easiest way seems to be to get them to shut their booklet when I go through the example. Even go as far as put it on the floor if necessary. Then they can open their booklet once I am done to try the Your Turn. I also make scans of the sheets available to students after they are complete, so I might get students to NOT copy the example in class, and then get them to do the example as a homework, where they can check against my version. This would give them another exposure pretty soon after the first, and give them instant feedback on it.

Rule - I have been playing around with Frayer Diagrams for a year or so too, and the Rule sequence is a nice structure to lead into these. So far I have been using them to introduce the definitions, but this has not really been successful. Flipping this and getting students to fill them in themselves after seeing a sequence of examples, non-examples and boundary examples is a much better approach. 

In out department​

I also want to get my department thinking more deeply about the questions we offer students and the experiences they get of thinking mathematically. I am hoping to get some time with the whole department to get them to do some sets of questions over the coming months, and then start building some of our own sets. I think I will start with the Reflect, Expect, Check, Explain cycle.

It is difficult as we are still in lockdown from Covid, but I think we can make it work via breakout rooms in Zoom. Thoughts and plans are coming together…

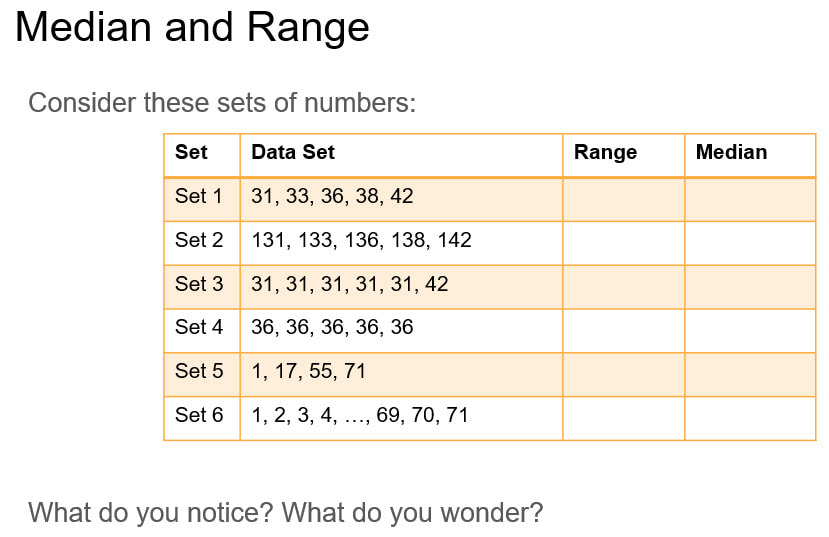
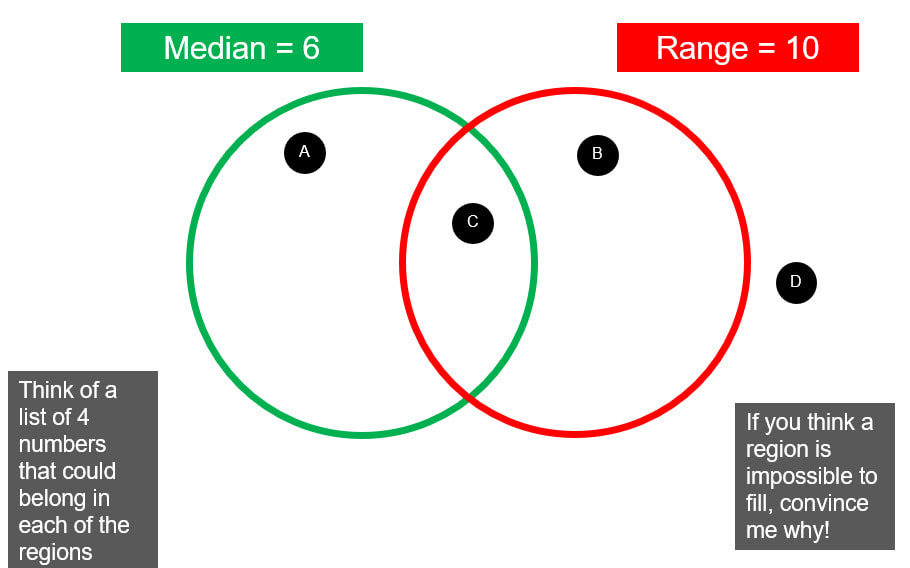
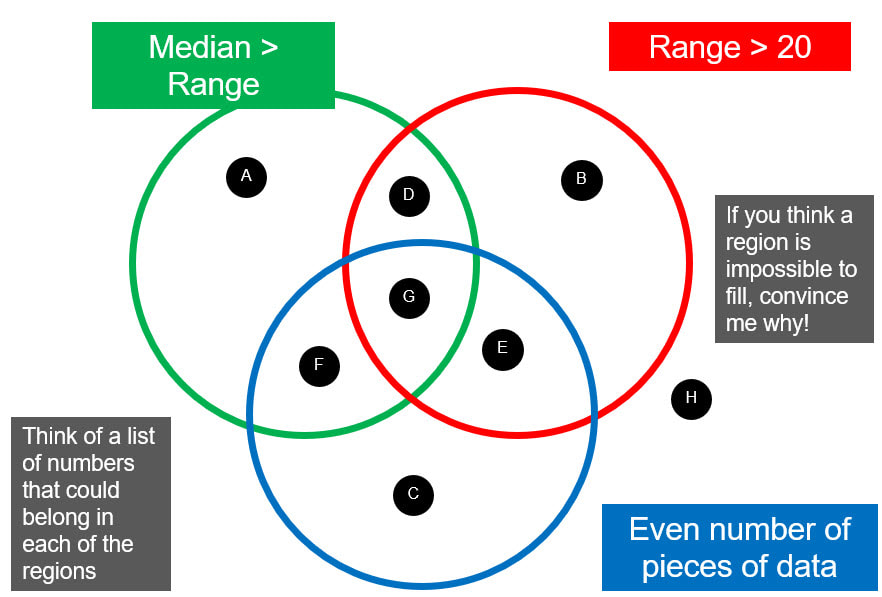
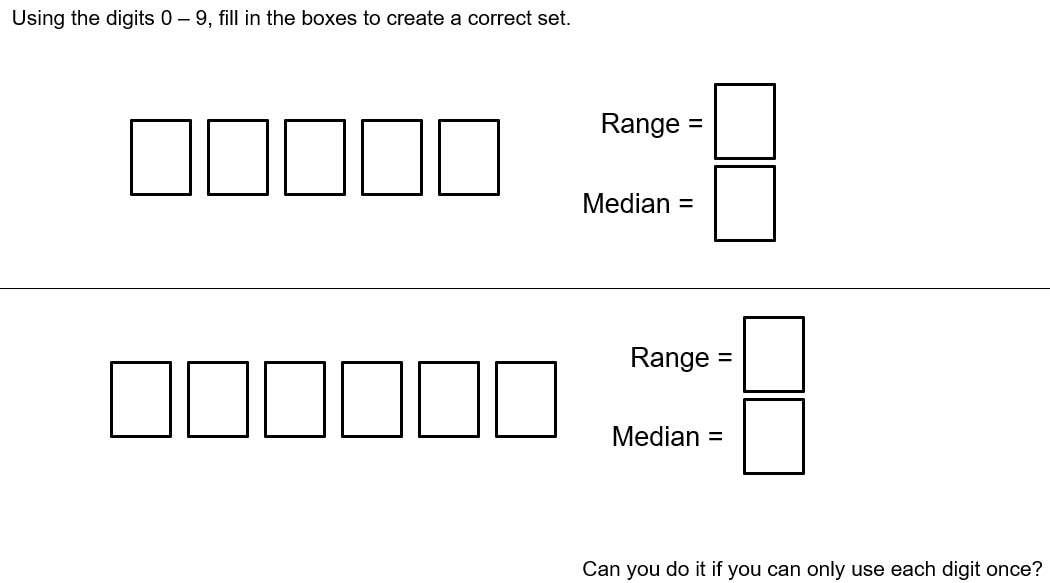
We have moved to using the White Rose schemes of learning this year. In the current unit on place value, I was surprised to see the inclusion of Range and Median as Small Steps in their guidance. But when I thought about it more, it makes perfect sense. Separate these similar ideas from mean and mode. Both these require students to write a list of numbers in ascending order, which has been covered a couple of steps previously, so they get more practice. We then move on to ordering decimals, so we can come back to range and median in that context, and again later when we hit negative numbers.

But when I was looking for some tasks for students to do to practice these skills beyond the worksheets that White Rose provide, I realised nearly all resources either cover just one, or the whole mixture of averages. So I went ahead and adapted a few resources to fit what we have covered.

The first is a set of questions that I put together to try to get students thinking about what it means when the data set changes and only one of the median or range changes. It is meant to lead them towards the idea that both a measure of position (median) and spread (range) are necessary when looking at data.

The second is a More Less Same grid (check out this website for more).

The third and forth are a pair of Maths Venns tasks.

The final is an Open Middle style problem.

The PowerPoint file that contains all 5 is here.

Our students are currently heading towards their mock examinations, and usually at this time of year I do an assembly with them to talk about effective revision. But this year we are all on lockdown due to COVID-19, and it seems unlikely that we will be back in school any time soon. 

So I decided to do something I have meant to do for quite some time: put together a brief guides for students and parents on how to revise effectively. I wanted to build in the elements that I usually present, which are all evidence informed, and present it in a way that would help students identify both why it is important and what they should actually be doing.

I have seen other similar ideas before (a couple are linked in the Further Reading section), and there is nothing groundbreaking in what is included. Mine is just another example that people might find useful to share with their students, parents and colleagues.

You can find a PDF version here (and the one with my school logo here) .