As a starter for my first year IB students I use a random question based on past exam style questions (my generator of these is here http://classes.interactive-maths.com/mssl-exam-qs.html). In this lesson I was using question 25, a topic that students find really difficult. Below is the actual question that appeared.
After some fumbling around, a few students were able to answer parts a and b, but they were all pretty stuck on part c. A couple of students had some initial ideas, so I asked them to share what they thought. I then informed them all that I could see at least 4 different methods for solving the problem using methods we had seen, two of which were put forward by students.
I asked the students to come up to the boards and start their solutions, even if they could not finish them. They both started correctly, and I continued the method, with questioning to the final answer.
Method 1 - Simultaneous Equations
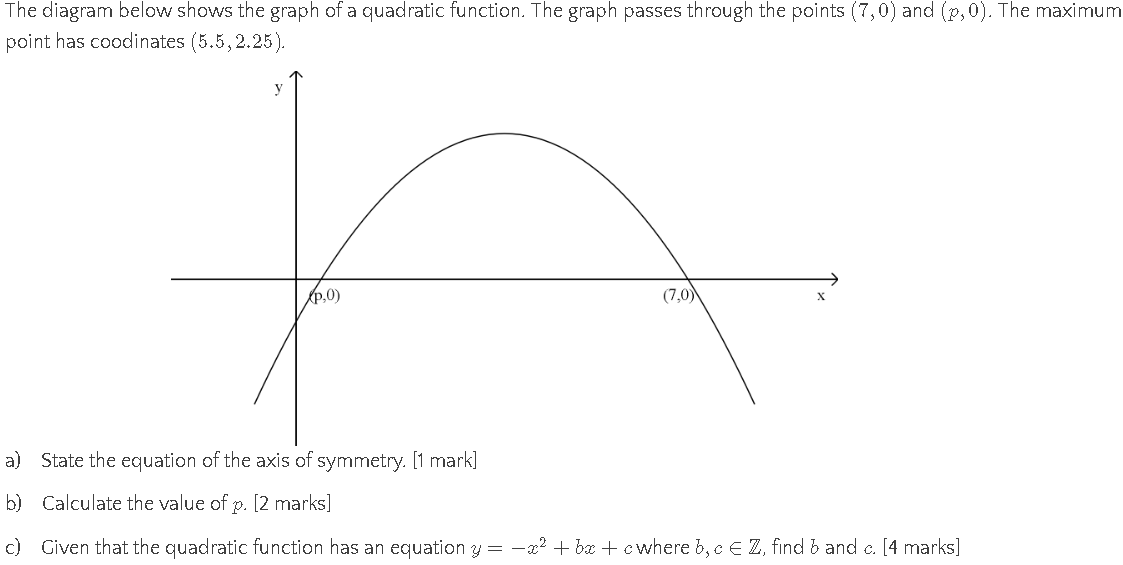
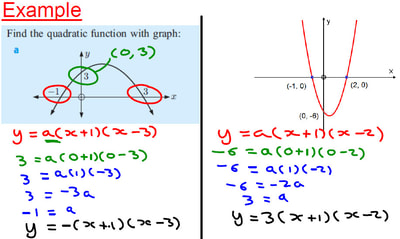
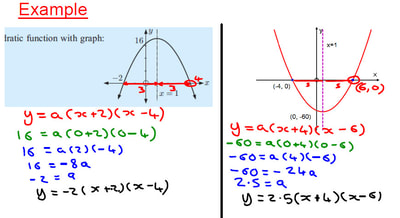
| The concept of substituting a point into an equation to find missing constants is one I have been pushing as it has wide applications across different functions types. This is the method we use to find the equation of a straight line when we know points. So it seems natural that this is also the preferred method. I also like the fact that it helps students realise the connection between the coordinate and the equation. Whilst going through this example I picked up on the difference between -4² and (-4)² and why it is the former in this case. At the end I also said there was a third different equation we could have used, and asked what it was. A couple of students spotted that they could have used the vertex coordinate instead of the roots. |  |
Method 2 - Axis of Symmetry
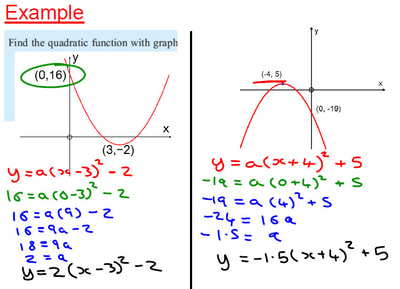
| Similar to above (in actuality it is just another version of a simultaneous equation), but making use of the formula for the equation of the axis of symmetry (they are given this in the formula booklet for IB Mathematical Studies), one student noted that as they know the value of a, this is fairly straightforward. But they got stuck at finding the value of c, which they had worked out by the time we went through method 1. |  |
Method 3 - Root Form
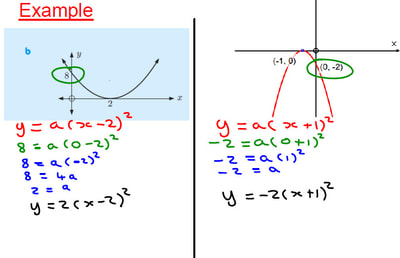
| This links to the work we did previously on Root Form, but many students could not recall the details of how to do this. I modeled the answer, firing a few questions on bits I knew they could do. I told them this is the method that I personally would choose to answer the question, but recognised that it relied on confidence in algebra (something they do not have). |  |
Method 4 - Vertex Form
| As above really. |  |
Although this starter ended up taking 30 minutes(!) it was a useful discussion to have. For the students, they got to see four different methods that would get them to the answer, so helped them realise there is not just one correct way to do things. And for me I got to see which methods they preferred, and which they found difficult.
I will be revisiting this question in a few lessons time to review it and see how well students can recall how to do it, and I will be challenging them to remember all four methods. This is one of the reasons I love randomly generated questions, as I can do the same skill but with different numbers really easily, and it also gives me a quick starter activity (with answers) for each lesson.
This is the process of how I have approached developing attacking exam style questions with this course, and it seems to have been working pretty well. When I teach the content, all the practice is on the basic skills, focusing on developing fluency and some understanding. Then after a couple of weeks I will use a starter exam question on that topic. This introduces some spacing and retrieval, and has given students some time to consolidate the new learning. By then returning to exam questions periodically for that topic, students get regular retrieval opportunities, and each time they are able to further develop their conceptual understanding, having had time to process the information.
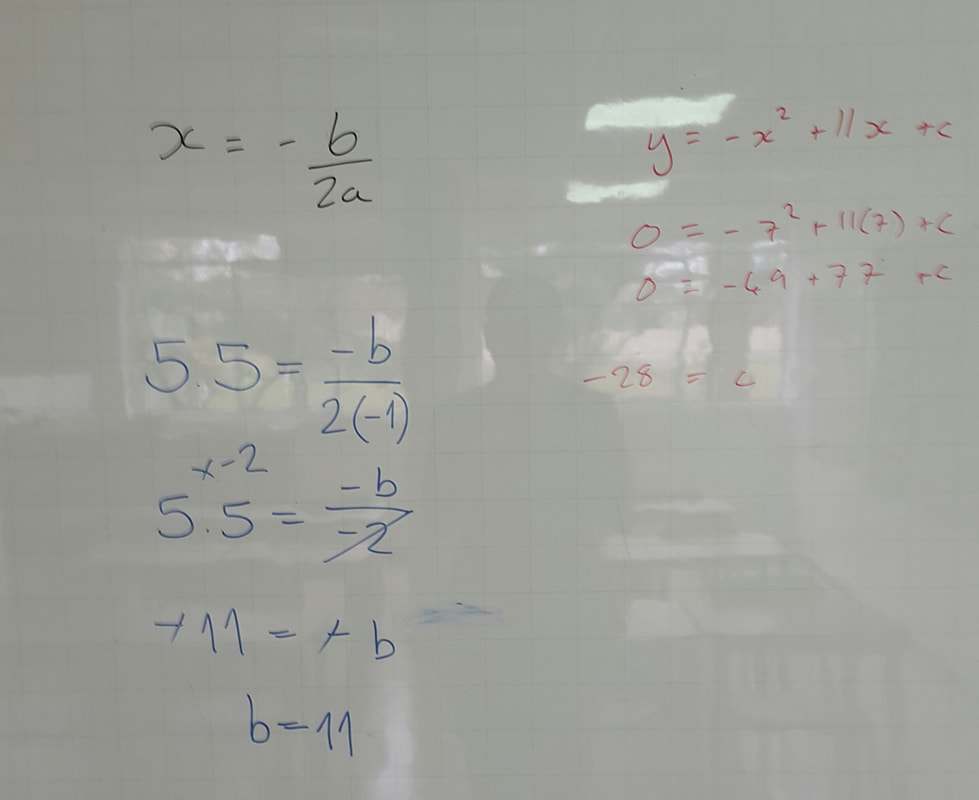
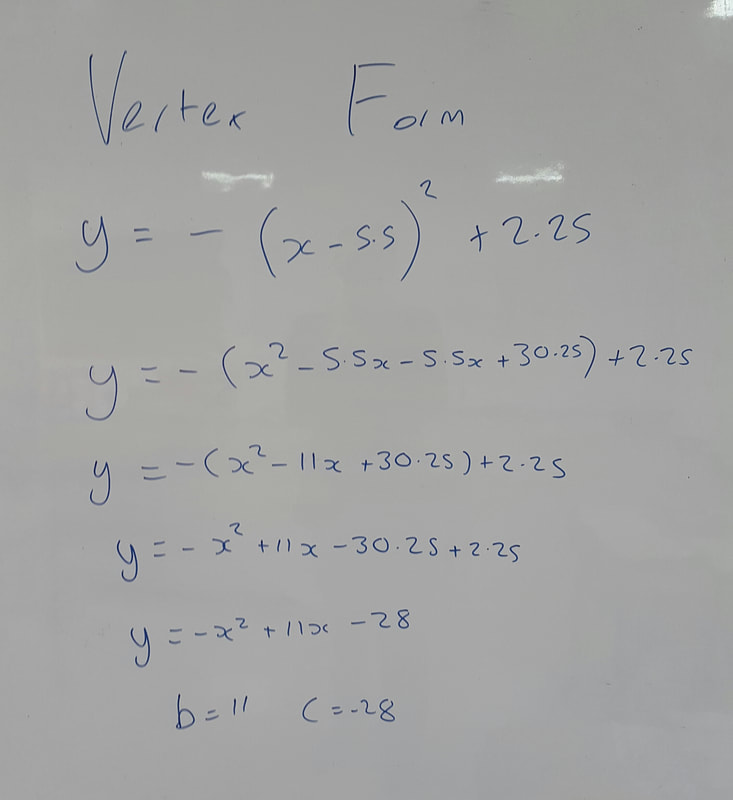
RSS Feed
