I have previously shared this padlet of links to blog posts on a host of different areas of Teaching and Learning. Hopefully it will prove useful to some people when trying to find posts from the edu-blogosphere. If you have any suggestions of headings, or blogs for me to include, then please do let me know (might be easiest to do this through twitter).
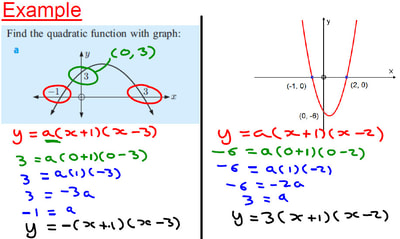
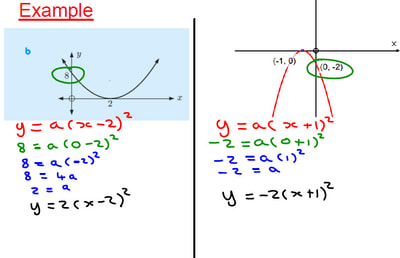
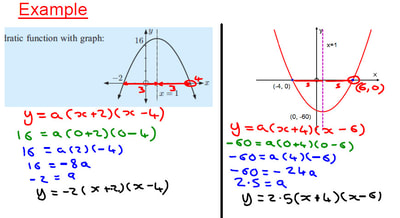
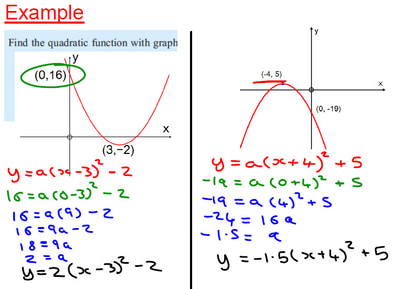
I have been trying to extend the use of example problem pairs to more of my classes, and have started to use them with my first year IB students. We were looking at finding the equation of a quadratic from a graph, having already covered sketching graphs given in root (factorised) and vertex (completed square) form.
I am a firm believer that exam groups need to get lots of practice of past exam questions in the final run up to the exams. Often this will involve doing lots of past papers in class, but to keep it a little bit varied I have done these two activities this week:
- Stick a question from the IGCSE paper 4 (these are longish questions broken down into steps) on each of the six whiteboards I have around my room. Students work in pairs to answer the question. Then they rotate and the next pair checks the work of the first pair. Markscheme is given out to check the actual answers, and students discuss any they got wrong. Groups rotate again to a new question. I chose questions on topics that appear regularly in this exam (percentages, trigonometry, graphing with their calculator, cumulative frequency, etc).
- A relay on the IGCSE Paper 2 (short non calculator exam, with 10-12 questions in 40 minutes). Each pair of students has to answer the first question, bring it to me, and if correct, they move on to the next question. To promote accuracy over guessing and speed, I used a factor of 3 if they got it correct on the first go, a factor of 2 on the second go, and a factor of 1 on the third go. I applied this to working marks too, so if they got 1 working mark in the first try and then the second mark on the second go, they would get 3x1 + 2x1 = 5 out of a possible 6 marks.
With my first year IB students I have been having a few issues with some of them doing the homework to an acceptable standard to help them recall. Too many were copying from friends/notes, rather than retrieving. So now I have started to do a quiz based on the homework. They hand in the homework (which is a double sided sheet of approximately 5 exam style questions from topics they have seen previously) at the start of the lesson, and, as before, they do the starter (an past exam question). I will then teach some new content. In the middle of the lesson I give them the quiz (it is a 80 minute double period). This quiz is the same as the homework, but with different numbers. I collect the quiz version, which I mark after class, and they self mark the homework.
I was put on cover for a P6 (11-12 year olds) Maths lesson. The lesson was on the unitary method of proportion, and I was taking the second half of a double lesson, which had already been covered by another Maths teacher in the first period. I walked in to a class struggling to apply the unitary method to an indirect proportion problem (12 workers take 20 hours, how many workers needed for it to take 15 hours). Although they had solved the problem, they were unable to explain why it worked, and my colleague was struggling to see how to apply the unitary method to this particular problem (being a cover lesson, he was caught a little off guard!). This naturally led to a bit of team teaching with my colleague (who has a very different teacher personality to me), with him working on a direct problem on one board and then passing to me to show the indirect problem on another board. The light bulb moment came for most of them when my colleague suddenly shouted "I got it! If it takes 12 workers 20 hours, then there is 240 hours of work! If my 11 friends didn't turn up, then I would have to do 240 hours of work all by myself".
The rest of the lesson I just chose questions from the set worksheet, put them on the board and challenged students to work them out in groups. But what I kept doing was linking it back to the words UNITARY, DIRECT and INDIRECT, and making comparisons between the problems as they went up on the board.
What's the first thing we have to do?
Find the unit!
How do we know it is direct?
As one goes up, so does the other!
How do we know it is indirect?
As one goes up the other goes down!
What was particularly fun about this lesson was that I "adopted" the personality of my colleague. This took to a way of teaching I haven't done before, and I can certainly see the benefits. Making a big deal out of things really helped it stick in their heads. It comes so naturally to my colleague, but this is certainly something I am going to try to pinpoint what he does, and incorporate it into my teaching a little.

 RSS Feed
RSS Feed
