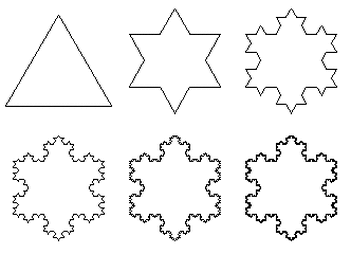
This year with my Year 10 class I decided to build a fractal christmas tree as given on Think Maths. However, before getting into the making, I wanted to explore the world of fractals with the class a little bit first.
I started by looking at the Koch Snowflake, and we found this by constructing it. We started with an equilateral triangle that had side length 9cm (a little revision of constructions), and then split each side into three 3cm sections. On the middle of each of these sections, we constructed a new 3cm equilateral triangle. Now we split each 3cm side into three 1cm sides, and again constructed a 1cm equilateral triangle in the middle section on each side.
The first 6 iterations of the Koch Snowflake
| 
Self-similar nature of the Koch Snowflake
|
We then discussed the nature of fractals and their self-similarity, and their applications to things such as coastlines.
We now had a look at the Sierpinski Carpet, and once again started by constructing it. First they had to construct a square that was again 9cm by 9cm. This was then split into a three by three pattern of 3cm squares, and the middle square was removed (or shaded in). Then each of the 3cm squares was split into nine 1cm squares, and again, the middle of these was removed (or shaded).
The first 4 iterations of the sierpinski carpet
Finally we moved on to look at the Sierpinski Triangle, and again started by constructing an equilateral triangle, this time of side length 16cm (or 8 cm if their compass was not big enough). We then found the midpoint of each side, and connected these three points to create a new (upside down) equilateral triangle. This was removed (or shaded). In the three remaining equilateral triangles, the process is repeated, joining the midpoints of the sides and removing (or shading) the middle (upside down) triangle.
The first 6 iterations of the Sierpinski Triangle
| 
A colourful completed Sierpinski Triangle
|
This was when I then introduced the main task, building a Fractal Christmas Tree. We briefly discussed the nature of turning each of these 2D fractals into a 3D version - the Menger Sponge and Sierpinski Tetrahedron. Then I split the class into groups to work on the different aspects of the Christmas Tree:
- The Koch Snowflake for the top of the tree
- The Koch Snowflake bauble decorations
- The Menger Sponge as the base/stand
- The Sierpinski Tetrahedron as the actual tree
In order to make the whole tree we needed 12 units of the Menger Sponge, 4 Koch Snowflakes and 64 small Sierpinski Tetrahedrons. After about an hour (split over two lessons), the tree was complete, and the final result is shown below.
This was a great Christmas activity, which produced a lovely finished product. I certainly enjoyed it, and the students seemed to as well. If I was to do it again, next time I would use some platonic solids or other 3D shapes as the decorations, and maybe make some smaller Menger Sponges to go underneath the tree like presents. It was a fitting activity to do as my final lesson with this class as well.
RSS Feed
