|
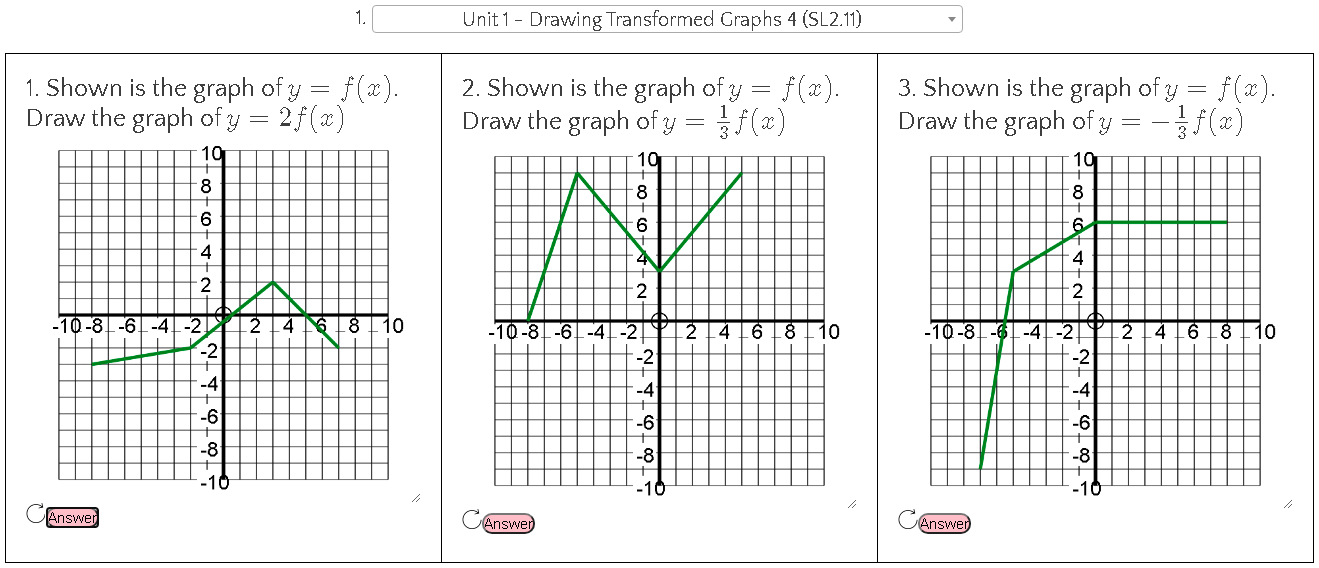
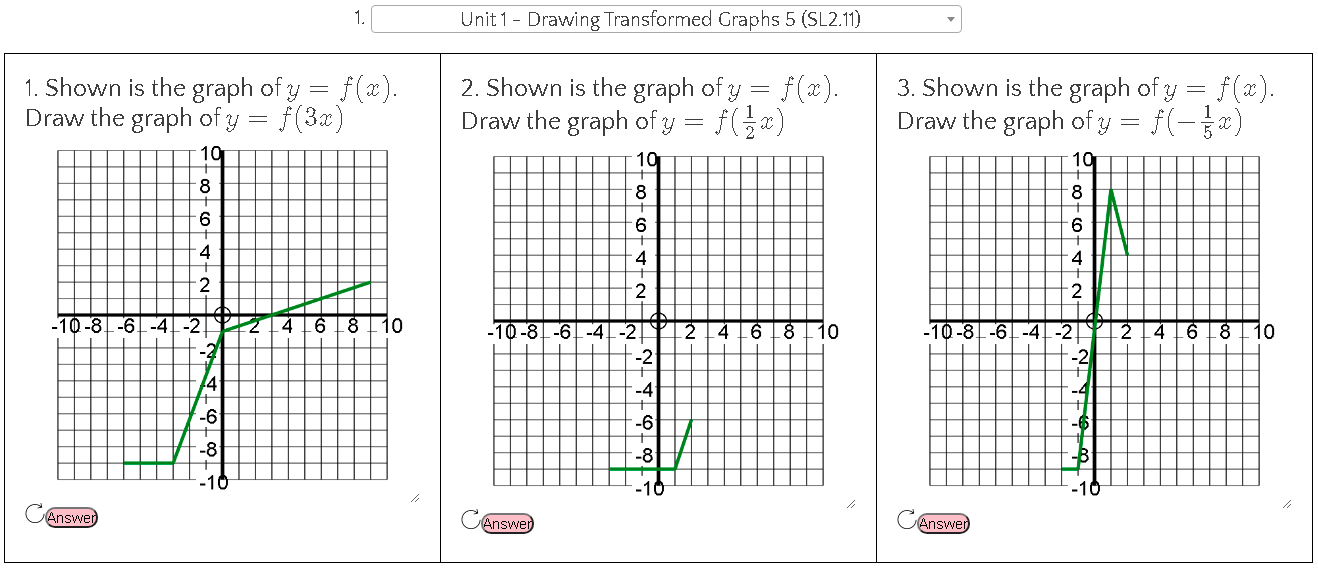
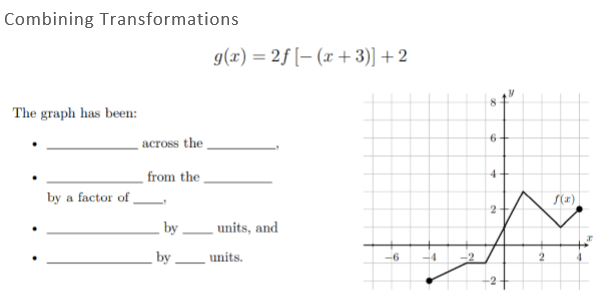
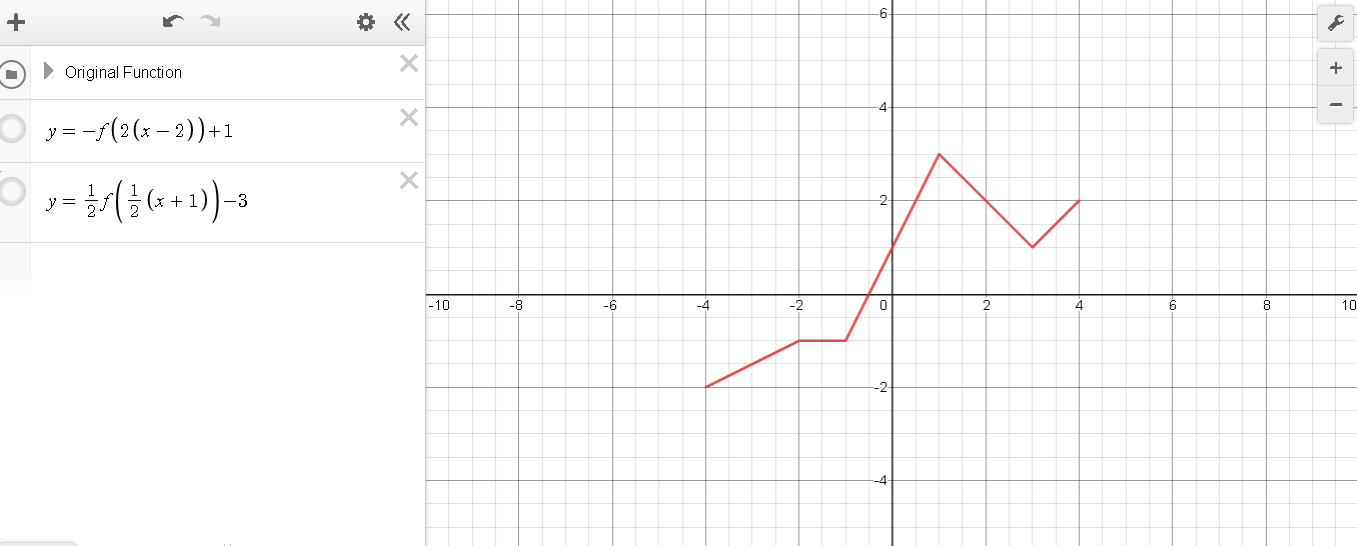
This week I had a breakthrough on how I could teach transforming functions to my IB AA SL students, which as with many of the best ideas, happened almost completely by accident! The lesson was on combining different transformations to draw complicated functions. The end point for the lesson was questions like this where you have a function f(x) and have to draw something like g(x) given below (f(x) was defined earlier in the example, and is shown in the graph). But from the previous lesson I knew that several students were still having issues with vertical and horizontal stretches, especially when the factors are negative, so I wanted to practice these first. I decided to use my IB Key Skills question generator to create 3 questions of increasing difficulty. We started with the ones shown below. This is nothing new. I often do this when I know there are problems for some students. It gives us a chance to discuss as a class the approach to different questions. But what I realised whilst doing this was that I could ask students to annotate on the screen to show their answers. I can't believe it has taken me this long to think of this, but it was equivalent to getting students to the front to draw on the board! Anyway, after kicking myself for not thinking of this earlier, I realised I could do a lot more with it. For starters, I had three students working at a time, and I chose students to work on the level of difficulty that I thought was appropriate for them based on the previous lesson. I asked the other students to work out what their answers would be. When a student had finished their question I asked the rest of the class to use the stamps built in to the Annotate function of Zoom, to either tick, cross or ? each answer. This gave me a feeling of what the class thought (and because I could see the names as they annotated, who was right or wrong). The ? was good too, as it allowed students to show they still weren't sure. For those that disagreed with an answer I asked them to explain why. After we had all three answers done, I pushed the answer button to show the answer. And what worked REALLY well, was when I then scrolled down, the annotations don't move. Usually this is a pain, but in this instance it was perfect, as the graphs they had drawn slid on top of the answers, clearly showing if they were right or not (all of them were by this point). This short recording gives an idea of the whole process. I made it after the lesson, so it looks like I am annotating, but in class it was students names that appeared. Of course, the benefit of randomly generated questions is that then I could create 3 more instantly and get 3 different students to have a go (this time choosing those who I knew had struggled last lesson, and had intentionally avoided in round 1). I only needed to do this twice, but I could keep going if I needed. Then with a quick change of settings we got these questions. After a few of those, we pushed into combined transformations with these questions, and I showed them the answer for the first one. I asked them to put their answers in the chat, and they all got it correct. We had to talk about the importance of the order of the transformations later, but that wasn't on my mind just yet. Then we moved on to look at this example together as a class (available in the lesson sheet for this topic). Which I colour coded as below Then I sent them off to try two Your Turn questions in pairs, suggesting they use the annotate function to communicate with each other as they worked through the problem. Finally, as the lesson came to a close, I wanted them to quickly check their answers, so I whipped up a desmos file to reveal the answers.
1 Comment
16/7/2023 08:53:36 pm
It is an informative blog that explores the fascinating world of graph transformations using the Zoom framework. The review commends the blog for its clear and concise explanations of graph transformations and how they can be applied in Zoom. It highlights the author's ability to break down complex concepts into digestible chunks, making it accessible for readers at various levels of familiarity with the topic. The blog effectively demonstrates the practical applications of graph transformations in enhancing the visual representation and functionality of Zoom graphs. Overall, it provides valuable insights into leveraging graph transformations to maximize the potential of Zoom as a data visualization tool.
Reply
Leave a Reply. |
Dan Rodriguez-Clark
I am a maths teacher looking to share good ideas for use in the classroom, with a current interest in integrating educational research into my practice. Categories
All
Archives
August 2021
|
|
Indices and Activities
|
Sister Sites
|
©2012-2023 Daniel Rodriguez-Clark
All rights reserved |
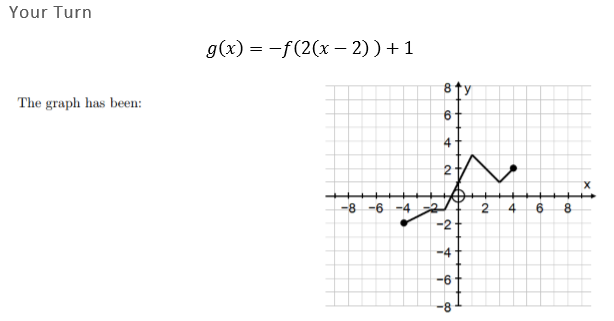


 RSS Feed
RSS Feed
