The second book by Craig Barton (well, ignoring the non Maths teaching ones) is everything a sequel should be: it builds upon the greatness of the first, but has its own tale to tell. It gets into the nitty gritty of the story, focusing on one of the smaller parts of the first. And yes, it is a bit controversial.

I am not going to write a summary here. I thought I was, but that would not be able to do any justice to the book. If you are a Maths teacher, you should read the book. Craig is open throughout about not trying to tell you what to do, but rather telling what he does, why he does it, and provoking you to think about how you could adapt those things to work for you (if indeed you find them valuable in the first place). But even if you disagree with everything Craig has to say, then you will still learn a lot from reading the book. If nothing else, if you do all the sequences of questions he provides, you will be giving your subject knowledge a good servicing!

Here I am going to share a few of my main takeaways, and what I want to incorporate into the book.

In my teaching ​

In the very last chapter of the book, Craig gives some advice on "Making it work", and the first thing is to choose one thing you want to try. Well, I am going to ignore him on that! Well, not completely. I am going to choose one thing that is new, and 3 things that I currently do but want to adapt after reading the book.

Reflect, Expect, Check, Explain - this is the new one. I have been using some sequences of questions from Craig's www.variationtheory.com website, as well as making some of my own, but, honestly, they have really just been a set of questions. They have allowed me to direct student attention to certain things, but I have not been systematic enough in my approach to develop their mathematical thinking in the way Craig describes. 

Since starting the book I have been adding some elements, in particular the reflect stage, but I want to make more of this. So I am going to try the full structure, and use the Prompt Questions that Craig suggests (available on his website: http://mrbartonmaths.com/booklinks/). I think I will need to use a template to help them structure the process too. My plan is to try this with my first year IB class, though I need to think carefully about what topic to do this with. We have some recap of indices and logarithms coming up, so that seems like a good fit. I will blog again on this when I give it a go. I have been using some sets of questions with them (such as the one below on Binomial Expansion), and have made short references to the ideas of reflecting on what has changed, but will need to be more explicit about this.

Another aspect that I have not been building in that Is important is the idea of Fluency Practice before the intelligent practice. I used to do too much fluency practice, now I am not doing enough for students to get the most out of these sequences of questions. For students to develop the mathematical skills, they need to be more confident with the method they need to apply first,

Atomisation - this is something I have been exploring, in particular with putting together the IGCSE Booklets and IB Lesson Sheets, but the systematic way Craig approaches it grabbed my attention. Going through the small atoms that make up a new idea and ensuring they are all secure first is something I want to look into further, but think that will definitely need to be a collaborative project. I am also thinking about how I could do some of that in the "flipped" model with IB classes.

Example problem pairs - just a minor adaption to my current process, but I need to find a consistent way to get all their attention on the example. I print examples and your turns in the booklet/lesson sheet, so the easiest way seems to be to get them to shut their booklet when I go through the example. Even go as far as put it on the floor if necessary. Then they can open their booklet once I am done to try the Your Turn. I also make scans of the sheets available to students after they are complete, so I might get students to NOT copy the example in class, and then get them to do the example as a homework, where they can check against my version. This would give them another exposure pretty soon after the first, and give them instant feedback on it.

Rule - I have been playing around with Frayer Diagrams for a year or so too, and the Rule sequence is a nice structure to lead into these. So far I have been using them to introduce the definitions, but this has not really been successful. Flipping this and getting students to fill them in themselves after seeing a sequence of examples, non-examples and boundary examples is a much better approach. 

In out department​

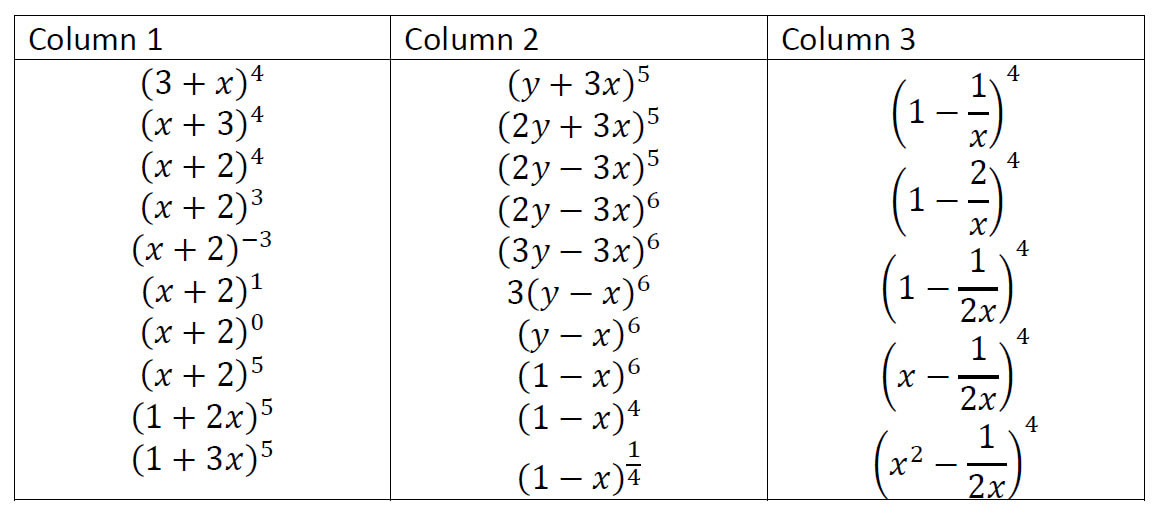
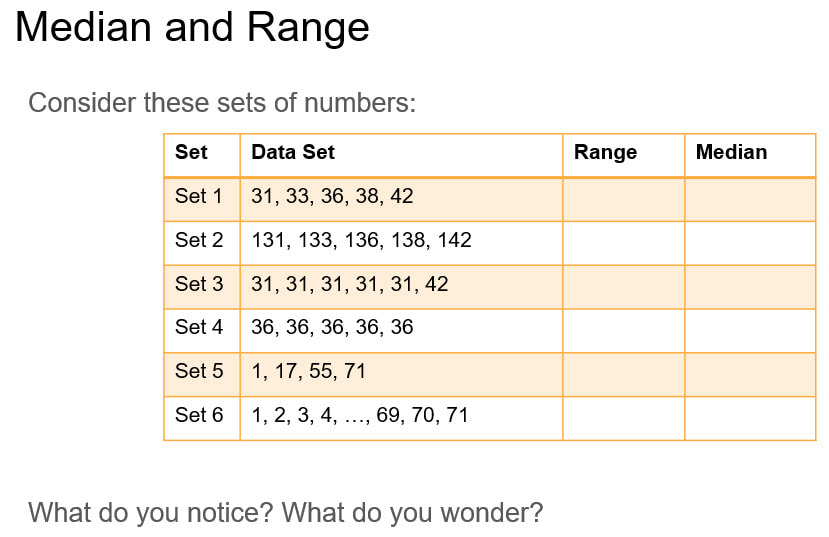
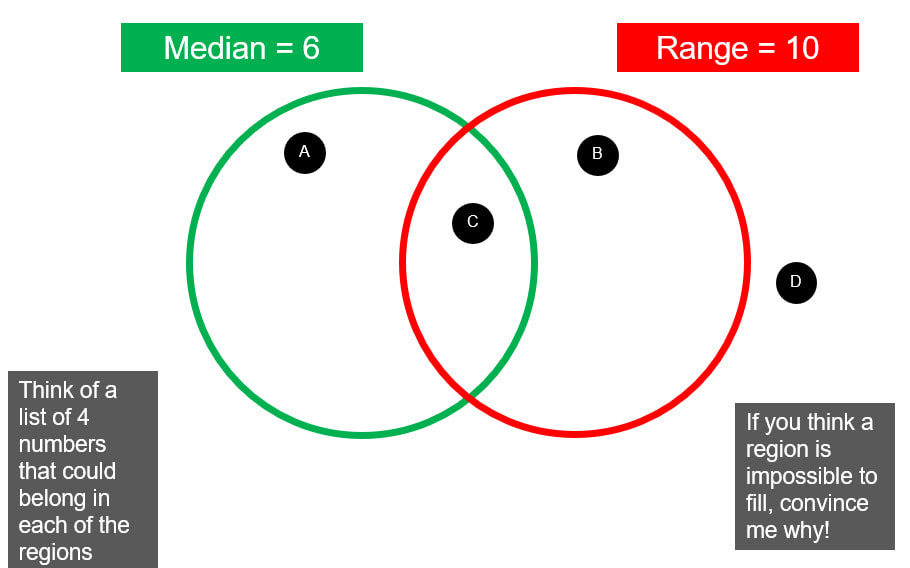
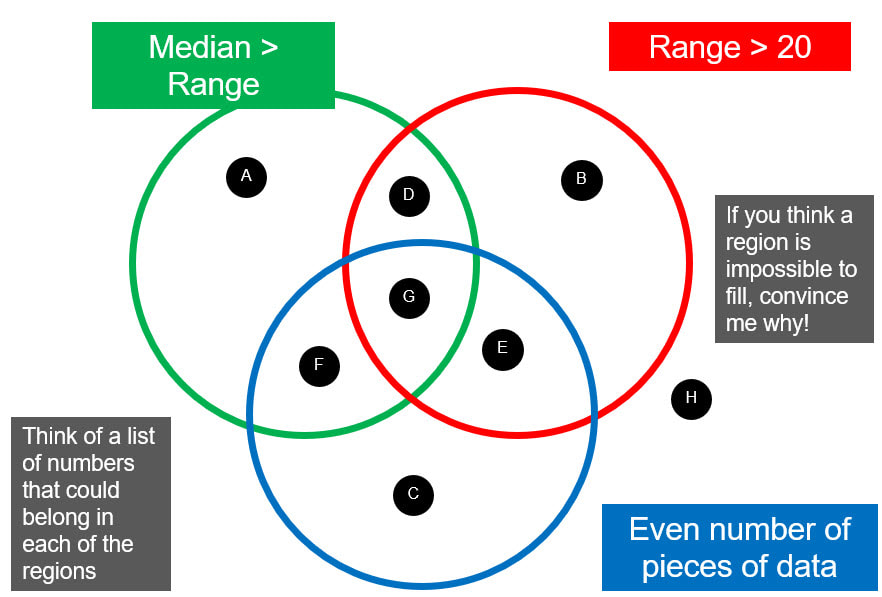
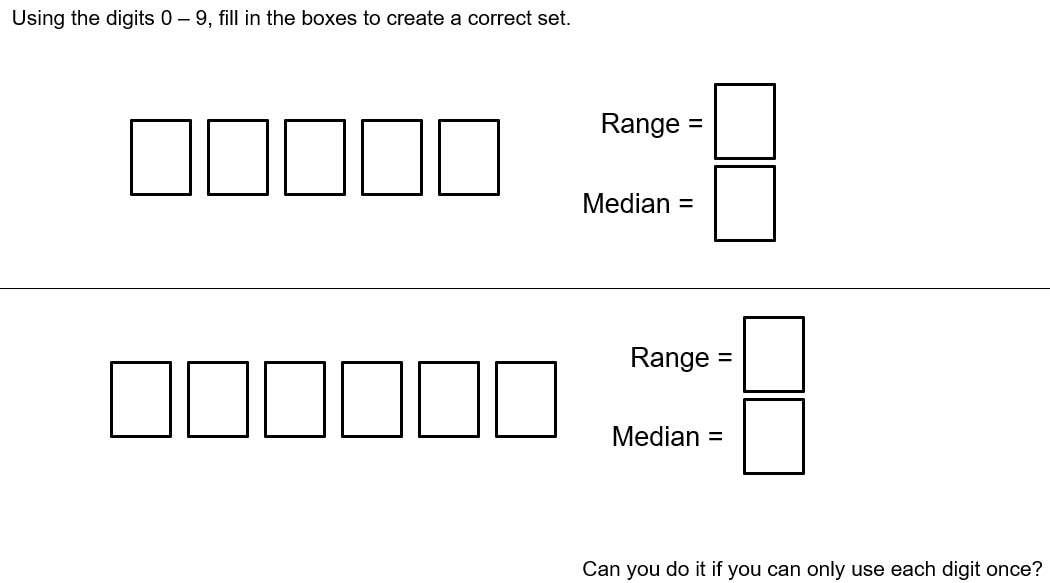
I also want to get my department thinking more deeply about the questions we offer students and the experiences they get of thinking mathematically. I am hoping to get some time with the whole department to get them to do some sets of questions over the coming months, and then start building some of our own sets. I think I will start with the Reflect, Expect, Check, Explain cycle.

It is difficult as we are still in lockdown from Covid, but I think we can make it work via breakout rooms in Zoom. Thoughts and plans are coming together…

We have moved to using the White Rose schemes of learning this year. In the current unit on place value, I was surprised to see the inclusion of Range and Median as Small Steps in their guidance. But when I thought about it more, it makes perfect sense. Separate these similar ideas from mean and mode. Both these require students to write a list of numbers in ascending order, which has been covered a couple of steps previously, so they get more practice. We then move on to ordering decimals, so we can come back to range and median in that context, and again later when we hit negative numbers.

But when I was looking for some tasks for students to do to practice these skills beyond the worksheets that White Rose provide, I realised nearly all resources either cover just one, or the whole mixture of averages. So I went ahead and adapted a few resources to fit what we have covered.

The first is a set of questions that I put together to try to get students thinking about what it means when the data set changes and only one of the median or range changes. It is meant to lead them towards the idea that both a measure of position (median) and spread (range) are necessary when looking at data.

The second is a More Less Same grid (check out this website for more).

The third and forth are a pair of Maths Venns tasks.

The final is an Open Middle style problem.

The PowerPoint file that contains all 5 is here.

Our students are currently heading towards their mock examinations, and usually at this time of year I do an assembly with them to talk about effective revision. But this year we are all on lockdown due to COVID-19, and it seems unlikely that we will be back in school any time soon. 

So I decided to do something I have meant to do for quite some time: put together a brief guides for students and parents on how to revise effectively. I wanted to build in the elements that I usually present, which are all evidence informed, and present it in a way that would help students identify both why it is important and what they should actually be doing.

I have seen other similar ideas before (a couple are linked in the Further Reading section), and there is nothing groundbreaking in what is included. Mine is just another example that people might find useful to share with their students, parents and colleagues.

You can find a PDF version here (and the one with my school logo here) .

I have been working on what I call the Aspects of Teaching, which is designed to underpin our Instructional Coaching Programme. The purpose behind this is to give coaches and teachers some broad areas of what we do to talk about, but also split it up a little bit to direct conversations to the most important parts that teachers want to work on.

Below is the Aspects of Teaching. It should start automatically, and takes about a minute to play through the whole animation. There is a static image version here.

Hopefully it is fairly self explanatory, which is why I have produced it in an animation form. But by splitting what we do into the 4 big Aspects, and then focusing on a particular detail within one of these, I am hoping to help create useful conversations.

For each Aspect there will be a set of strategies taken from various sources, including

• High-Impact Instruction by Jim Knight
• Teach Like a Champion 2.0 by Doug Lemov
• Making Every Lesson Count by Shaun Allison and Andy Tharby
• Teaching WalkThrus by Tom Sherrington and Oliver Caviglioli

These strategies will be used in the instructional coaching process as possible ideas that teachers could try to meet their goals. The next step of the process is to put these strategies together, and share them with the coaches so they can start to become experts in them.

I have just finished reading A Compendium of Mathematical Methods by Jo Morgan. It is a book directed at Maths teachers and has a simple purpose: sharing different methods that are used to perform some common processes that we teach.

For each of 19 topics, spanning the whole of secondary maths, Jo goes into depth on a variety of methods, always using 2 well chosen examples to show some of the subtleties you might otherwise miss. Accompanying this are some of her own notes, and excerpts from historical textbooks to show how these were approached in the past.

Jo stays neutral throughout the book, never saying one method is the best, but rather  presenting them as they are. A few concerns about some methods which rely on following a procedure rather than developing understanding are raised, but not in a judgemental way. The tone throughout is one of trying to start a conversation about mathematical methods.

When we come out of lockdown, I am going to take some of the chapters to my department to discuss. I think it is a great idea to talk about the merits of different methods, and looking at ones we don't use will help teachers develop their own subject knowledge too. I am also a fan of being consistent across the department in the main method we teach. I think this has benefits when students change teachers, and allows for more continuity. As we are a 3-18 all through school, we could even extend this to the primary school to discuss how we teach the foundation skills.

In terms of sharing methods with students, it is also nice to have a few other methods "up your sleeve" for those situations when they do not understand the primary one you use. Or with those who need an extra push, asking them to see if they can understand why different methods are actually the same can push their understanding. Perhaps using a method comparison example like Emma McCrea discusses in Making Every Maths Lesson Count could be used.

One thing that the book has made very clear to me is that we need to move to an area model of multiplication. It is a versatile and easy to understand method for multiplication, that can easily be extended to more complex topics such as algebraic expansion and factorising. I will be taking this to our department soon as I think this is something we should be consistent about.

It is a great read for any Maths teacher. It is not something that you need to read in one go, and perhaps is better read by chapter when you want to look at a particular topic.

And I am with Jo. Let's talk about methods. 

I am writing this as we are in the middle of the global Covid-19 pandemic. This has shut schools across the globe, leaving most children to be taught remotely. I have blogged before about how I have used Online Live Teaching in this situation. 

But one of the things that seems to be on everybody's mind is how do we get students to engage in this type of teaching. Without having students in the class it is much more difficult to judge engagement, and for some it is even difficult to ensure they are present and doing the work.

This raises the debate over what we actually mean when we talk about engaging students. As a younger teacher, I firmly fell into the camp of believing that lessons should be fun in order to motivate students to be engaged in lessons. I would spend hours designing activities, be it card sorts, bingos or jigsaw activities to keep the students busy and active throughout the lesson. My thinking behind this was that if they were kept busy, then they would be engaged in the lesson. 

Well, if I am being honest, I do not really mean "my thinking" in that last sentence. I mean "I was told/led to believe". Not necessarily directly, but certainly through the types of activities we were shown in my teacher training. These were the activities that were modelled to us, and so these were the types of activities that we employed in our teaching. And it was all about that holy grail of education: student engagement.

For those first few years of my career my job was to engage the students in the lesson, usually by making it fun in some way. Perhaps that was through the way I "performed", or through the activities I prepared. But my main concern was that students enjoyed lessons.

But now I see things differently. 

I still believe in engagement. We know from plenty of research that it is vital that students are engaged with the learning in order to learn the material (for example, check out MARGE by Shimamura). But there is a subtle but important difference in the language. You may not have noticed it.

At the start of this post I referred to students being engaged in the lesson. Now I am saying that students are engaged with the learning. 

And that is the crux of the issue when it comes to discussing engagement. Is our job to create engaging (fun) lessons? Or is it to make the content that students need to learn engaging? These are very different things. You could argue that the former is easier (though the workload was killer!) in that it requires far less thought on everybody's part. But again, that is the problem. As Willingham says, "memory is the residue of thought", and if we want students to remember things, we have to get them to think deeply about those things. And interestingly, this normally piques their interest and gets them engaged in the lesson.

So in this time of remote teaching when we are all concerned about keeping students engaged in their school work, think about this: do you want students to have fun, or do you want them to learn something? If it is the latter, perhaps you would be better off thinking hard about the content you want them to know, and, more importantly, how you can get the students to think really hard about it. Engage them in the learning, and they will be engaged in the lesson.

Online Teaching
I feel like I am in the routine of teaching online now, after 8 weeks. It is not ideal, and I would rather be in the classroom, but given the situation I think I have found my flow. There are still some things I need to focus on improving:

1. Involving all students in the lesson. Some students don't really engage by asking questions so Cold Calling is even more important in this situation. All students must be participating for me to hear their voice.
2. Smaller tasks. Especially with the younger students, some are struggling with the longer periods of individual work, and are drifting off task. I think it would be better to break them down and do a couple of questions, then feedback with the whole class. Normally I would wander round and talk with those students individually, but that can't happen now.
3. Explore Desmos. Many people have mentioned how good the teacher dashboard is in desmos. Whilst I have used it for the premade activities, I have never made one of my own, so that is the next step.

Key Skills
I have been thinking a lot about the key skills of my students, especially those I am teaching in the IB AA Standard Level course this year. I have started to put together a generator with these key skills at different levels, which I can use as a starter, to create worksheets, or at this time, get students to use it independently to keep overlearning these key skills so they can do them fluently.

Reflect, Expect, Check, Explain
A full post will come on this once I have finished reading the whole thing, but as I get close to finishing Chapter 1 (which could be a full book in its own right), I have already been struck by the amount of thought that Craig has put into this process.

I am planning to ask my HOD to bring the Estimated Means sequence of questions to a departmental Zoom meeting soon so we can all do them and discuss the benefits of these kinds of connections.

The structure of Reflect (what has changed), Expect (what do you expect to happen), Check (do the algorithm to see if your expectation was correct), Explain (can you explain the relationship) is a really helpful way to think about mathematical thinking. This is the behaviour we go through when answering questions, so we need to explicitly teach our students this behaviour too.

I am excited to try some elements of this out in the next few weeks.

CPD
There is soooooo much CPD available at the moment. Seneca Learn courses. ResearchEd Home videos. The usual blogs and articles. Books piling up. Complete Maths webinars. Inner Drive Academy. And with a 2 year old at home and teaching a full timetable via Zoom, I am not managing to get much done (other than slowly working my way through books). Keeping track of all the opportunities is difficult, and I want to do them all, but I just need to file them and come back to them when I have the time.

Instructional Coaching and Playbook
We launched our new instructional coaching programme in February this year. 3 weeks later, the whole of Peru went into lockdown, and coaching hit the backburner as we all got our head around teaching from home. But now I am trying to restart the programme in some way. It is difficult to get people on board when you can't go and speak to them directly about the possibility of being coached. I am relying on people letting me know when I keep mentioning it.

But whilst I am waiting for somebody to coach, I have made a start on putting together an instructional playbook (as Jim Knight calls it). This is the set of instructional strategies that the coaches become experts in so they can share them with teachers. I will be pulling on three books to bring it together: High Impact Instruction by Jim Knight; Teach Like a Champion 2.0 by Doug Lemov; Teaching WalkThrus by Tom Sherrington and Oliver Caviglioli.

But before pulling the actual strategies together, I have started by thinking about how I want to break them into groups. Each of these books does this, and I thought hard about our context and what groupings would work for us. I came up with this model, which also fits with our Principles of Great Teaching.

Teach Like Nobody's Watching by Mark Enser is a call for teachers to take control of their teaching, rather than pandering to outside entities (be it Ofsted, SLT, parents). It is based on two underlying principles: that we should do what is effective (do things that work) and what is efficient (don't do things the long way if there is a shorter way). It is the antidote to the fads of education: things that either don't work (teaching to learning styles), or have been morphed from what does work in such a way to make them useless (plan lessons in three parts), or they do (partially) work but are not worth the time investment in most cases (discovery models of learning).

Efficiency, as the author points out, is a term that is often viewed with disdain in education. "There is no place for efficiency in schools" is something I have had said to me, implying that efficiency is about stripping back and reducing the level of education. But that is not what efficiency is about. It is about reaching the same level with the least possible resources wasted. Those resources are not paper or electrical devices. Enser is talking about time costs of certain tasks. Every minute of teachers time spent doing something that could have been achieved in less time is time not used to prepare lessons, feedback to students, improve their own practice. Being efficient is about using our time wisely to achieve the best results, in the shortest time.

And Enser argues that an efficient and effective teacher follows four stages. He compares these to "real world teachers", such as driving instructors, who follow these stages naturally.

There are a lot of benefits to having a simple structure around which to base your teaching: it is easy to remember, meaning you are more likely to do it; it cuts out unnecessary stuff that has little impact on student learning; it reduces teacher stress and workload, and so makes them better at their job.

In Part 1 of the book, Enser goes into detail on each of these four aspects of effective and efficient teaching, linking to research and classroom practice. There are some suggestions for activities, but mostly it focuses on why these are important and the guiding principles of each.

Part 1, which is about half the book, is, in my opinion, an essential read for all teachers. It overviews what simple, effective and efficient teaching should be based upon, and gives teachers the springboard to take control of their own practice. It celebrates the classroom teacher.

Part 2 moves on to look at the curriculum and assessment. It looks at the taught curriculum and how we sequence it, the "super-curriculum" of things we want our students to know/experience/learn outside of structured lesson time, and how we can go about assessing if we have been successful at this. Again, all these are addressed from a viewpoint of being effective and efficient, and not wasting time on tasks that do not improve the learning of the students. 

The final chapter in part 2 is all about running department meetings and how to use them to develop one of the most important parts of great teachers: their subject knowledge. This chapter in itself is a must read for any head of department (or line manager to a head of department) as it is a treasure trove of simple ideas to help make departmental CPD time more effective, and less based on administrative tasks.

Part 3 looks at the wider school, and what role school leadership has to play in allowing teachers to do their job without interference. The thorny issues of behaviour, data tracking, non-negotiables, CPD and feedback policies are tackled, with Enser again arguing to cut these back to what is actually useful for teachers. Each of these is accompanied by a short case study from somebody in a leadership position from schools across the UK.

The whole premise of the book is to allow teachers to Teach Like Nobody's Watching, and at every turn Enser brings our attention to things we do which are not essential, and the things we could be doing that would make us more time efficient in doing our jobs. 

Making the time to read this book (and reflect on it) would be an effective and efficient way for all teachers to keep improving what they do, and help our students do the best they can.

My Takeaways
The simplicity of the recap, input, application, feedback model of teaching is great. I have been guilty of over-complicating things in the past, both as a teacher and T+L leader, and this call to simplify what we do has struck a nerve with me.

My teaching does (now) largely follow this approach, though reading this has made me more aware of the importance of each stage. It can be easy to skip recap, for example, when pushed for time. But building in the stereotypical "Last lesson we..." has been something I have implemented immediately, even in live online teaching.

But here are a few highlights from each chapter:
Recap - importance of connecting new learning to old material explicitly; Cornwell notes; show students the puzzle box to help them fit new knowledge in the right place.
Input - requires attention and good behaviour; the importance of good subject knowledge; limits on working memory; dual coding; interactive through questioning; don't rush!
Application - get students thinking hard; break it down and bring it together; ensure understanding before application; make the task focus on what you want them to learn; importance of modelling; is the purpose of application to perform or to practice.
Feedback - feedback is not the same as marking; reduce the need for feedback (careful input, give success criteria); reduce time (verbal, whole class); make it count (have a purpose, action points, make it specific).
Programme of Study - the curriculum is the journey you wish to take your pupils on, so make it a conscious choice; build upon previous knowledge; identify and keep coming back to threshold concepts.
Super-curriculum - avoid a scattergun approach and link to the main curriculum; increase cultural capital with general knowledge within classes; better than a reading list is to set reading homework and link to curriculum.
Assessment - designed to make learning visible; be careful about what you are assessing (does language cause the issues); consider the types of validity (does it cover everything, would two tests on same topic produce same results, would a test on something different produce different results); benefits of rank assessments.
Department meetings - develop subject knowledge (audit, address gaps, adapt practice); develop curriculum (question, map, evaluate); common culture (expectations of student work, collaborate).
Leaders supporting teaching - it is impossible to teach well when there is poor behaviour; there needs to be an understanding of principles to avoid cargo cults; separate CPD from meetings and focus on why before handing to departments. 

In terms of leading T+L, the model has given me an idea for developing our new coaching programme, which I will write about soon. It has also made me reflect on the overly complicated nature of our own Principles of Great Teaching (...) which contain 16 different aspects. I wonder if collecting them under bigger terms would be useful? Again, building this in to the Coaching programme is on my to do list. This year was meant to be about departments going away and looking at how the Principles fit in their subjects, and what they look like, but the lockdown has pushed that back. I still need to ensure these conversations are happening when we get back. 

There has been plenty of debate on twitter the last few days over the effectiveness of teaching live online lessons vs setting work for students to complete in their own time. In other words, whether we should be teaching in a syncronous or asynchronous way in the current school closures.

Mark Enser goes into detail of why he thinks the asynchronous model is a better approach here as a response to some rather antagonistic tweets from a former Schools Minister. Enser accepts that different circumstances will mean that each model will be more effective in different situations. At the end of the post he asks for anyone who has been teaching live online lessons to share how they have made it successful, so that is my plan for this post.

My situation
First I want to state that I know that what I am doing would not work for everybody. Even those in a similar school situation have different home lives. I am not sharing this to say others should follow my lead, but rather that here are some things that have worked for me.

At the start of the lockdown I posted a blog with 5 tips. I stand by those now, though there are certainly things I might add!

As I write this we have been doing online teaching for 7.5 weeks since the schools were closed here in Peru. This started 1.5 weeks into our new school year. We are currently on a week's break before starting the second term of 9 weeks which will be done online too. It is very possible we do not return to school premises until 2021.

I mention this to make it clear that we are in this position for the long term, and so suggestions of just reviewing and mastering content students have already studied are not appropriate for us.

I work in a private school. This brings two things into the mix. Firstly, our students largely have their own devices (year 9 upwards all have laptops in school normally, and years 7 and 8 use them in certain lessons, so most also have their own) and Internet connections are not an issue (well, no more than are usually an issue here). Secondly, our salaries are dependent on parents continuing to pay the fees, and so there has to be a large element of 'pleasing the customer' at this time (more so than usual).

In terms of my technology I have a work laptop which I am using for the Zoom call, and then have my personal laptop set up beside this so I can do registers, see classkick progress, view the worksheet without having to jump between tabs on the work laptop. This has been an incredibly important part of my work flow solution.

Working at a private international school also has an impact on the number of periods we teach. We have 40 minute lessons and there are 40 periods a week. The maximum teaching load is 28, and most do not have more than 25/26. I also have a post of responsibility so have a lighter timetable.

I have a two and a half year old at home. He has not been able to leave the house for 7 weeks and is going stir crazy because of it. But fortunately my wife stopped working when he was born, and so she is taking the brunt of looking after him. Of course, he doesn't completely understand and finds it hard for me to be at home and not be able to see me, and this does lead to some interruptions.

But my school have been incredibly understanding of home situations from the outset. We are sticking to the normal timetable, and the only requirements on staff have been that they must have at least one live sessions with each class each week, and they should be available during timetabled class periods, but this can be via email/Google Classroom.

So given that many of the practical problems with live teaching are not an issue for me, I have decided (as have our whole Mathematics department) to teach all lessons live through Zoom.

What I am doing
This year I am teaching two year 7 classes, a year 12 IB standard level class and a year 13 IB Higher Level class. I have taken a different approach with the different age groups, but I do a Zoom lesson every period.

With the IB classes I have broadly followed what I do in school normally. As we are working towards and external qualification, there is an element of needing to cover the content, and this is taking a little longer than it normally would. I have cut the retrieval starters down for this reason, doing one question in single periods, and then following the Spacing Concepts I started this year in the double period.

In terms of the rest of the lesson, I am still using the lesson sheets I produce for IB classes. Students either print these or have them open of their screens and write in an exercise book if they have no printer. I do not have a printer at home, so I am writing in an exercise book.

I use my visualiser and screen share with the class my book, and work through examples as I do in class. Sometimes I will bring out a mini whiteboard under the visualiser to answer tangentially questions. Then students do a your turn. Where in class I can wander around to see their work, in Zoom I am making more use of cold calling students to talk through their entire solution, and asking if anybody did it differently. For shorter questions I get them all to type their answer in the chat function on Zoom, which I have set so that only I see their responses.

I am more reliant on them asking for help than I would like, but it seems to have worked well, as the quieter students are asking through the chat.

After some input, they generally work on some independent practice. I am making use of Classkick (I made this guide for our staff) and Desmos activities which both allow me to see student responses, but mainly for IB they have questions to do from the textbook, which have answers they can check. One of the mistakes I made early on was not ensuring they knew where the answers were, but now they are in the habit of checking themselves.

Keeping them on the Zoom call but muted has become the norm here. This was a request from the students who said they were too easily distracted working in their rooms without it. This also enables them to ask questions if they get stuck, and sometimes I will put them in a Breakout Room to discuss it with somebody else from the class.

With my year 7 classes I am taking a different approach. I am uploading a presentation to Classkick, and producing an assignment in Classkick for each lesson (labelled week 7 lesson 3 etc). The first slide is the starter activity which is Numeracy Ninjas. I have found this more important for the younger students as they arrive to the Zoom call in dribs and drabs, and this gives them something to do straight away. One benefit of Classkick is that I set it to mark automatically after 5 minutes.

After this I will usually introduce the idea for today's lesson through an example. I have mostly been doing this by editing the Classkick assignment live. If they are on the page they see my edits appear immediately. I then talk through these on the Zoom call. Whilst doing this I lock the assignment in Classkick so they cannot edit it. Then they do some practice. This will probably involve some your turns first which I check before they can move on to the main exercise (in Classkick they can call me to check their work). The main exercise is from the White Rose Maths resources (we changed our scheme of work to theirs this year), and I have set it to self mark where possible. I then keep a view of the whole classes work and can see their work live. I will check questions that can't be self checked (written answers) and answer questions which they can ask through Zoom or Classkick.

Some concluding thoughts
Some of the benefits of doing lessons live have been:

• Less work out of class as I do not have to mark every piece of work submitted. I can keep on top of this during class time like I would in school.
  
• Students can ask questions when they are stuck or unsure, like they would in class.
  
• I can monitor misconceptions more easily and address them earlier, through classkick and targeted cold calling. Again, more like being in school.
  
• The social aspect for our kids is important. They have not been able to leave their houses for 7 weeks now, so the normality of school and social interactions is really important.
  
• The kids and parents have asked for it. I have sent a couple of emails to parents explaining my process at this time. I have also sent a survey to kids and their parents. My school is doing the same on a whole school level. In all cases, the majority want Zoom classes if possible.

As I said at the start, I am not saying anybody else should go down this route, and I accept that the practical limitations could get in the way of this being a reality for many teachers. But I have found a way to make it work for me, and I feel like I am able to meet the learning objectives for the students this way in a more effective way than through an asynchronous model.

The biggest problem with online teaching (in either model) is checking for student understanding at the time of input. Through Classkick, questions and answers through Zoom chat and cold calling explanations of answers I think I have managed to make a good stab at being able to do this fairly effectively.

This year I have started trying something new with my IB class to promote their retention of key facts, concepts and skills. I have previously blogged about using the Last Lesson, Last Week, Last Unit, Further Back starters but having had our teaching time reduced I now struggle to feel these are a worthwhile use of time every lesson, and instead have moved to weekly quizzes made up of past exam questions. They get the same number of questions but I mark them and we 'waste' less lesson time in transitions.

But I still wanted to do some daily recall (it is a Rosenshine Principle after all!) and with this particular class was a little worried about their knowledge and fluency of key terms and basic skills. I decided to keep a track of the new vocabulary we meet in class, along with key facts and any simple key skills. That is, the things I want them to be fluent in doing. 

On top of this, I wanted a more systematic way to review these things keeping the spacing effect in mind.

To do this I created a spreadsheet!

I input the concept/fact/skill into the first sheet and it automatically copies across into the Review Timeline sheet. Then I enter a 1 in the cell that matches when I first taught the concept to students. So in the first lesson of the first week I taught them the concept Gradient and how to find a gradient (The ones before were taught in the taster sessions last year).

The sheet then automatically populates the rest of the row with when to do the next review. So the following lesson is a 2 which is the second review. After three more lessons, the 3 tells me when to do the next review. A larger gap appears before the 4th, then 5th, 6th, 7th, 8th and 9th review sessions. We teach the course over six 9 week bimesters, with a final bimester of revision before the exams, so I have set it up for those 6 bimesters. Not all topics are going to get the full 9 reviews, but for gradient the final review occurs in Week 8 of the fifth bimester at which point there is a full 9 weeks between each review.

Then for each lesson I look at the lesson we are in (Bimester 1 Week 5 Lesson 2) and look down the column to see which concepts etc I should review. 

With the current remote teaching I am assigning these as the starting activity as a Google Form for students to do as we wait for everyone to arrive in the Zoom class. I then check their answers and return it using the Google Forms features. My plan is to also increase the difficulty of the skills questions as the review stage increases.

When we go back to teaching in a classroom (which seems like it may still be a while off for us here), I am thinking about the best way to do this. It doesn't need to be at the start of the lesson.

If you would like to adapt this for your own teaching there is a template version here. There is a template version for having 1, 2, 3, 4 or 5 lessons a week. But you might need to adapt the headings for your situation. I suggest only adding extra columns at the end, rather than deleting columns in the middle, as this will mess up the formulas.

Obviously, this could be used to schedule a lot more than key concepts etc. Perhaps you could give it to students to help them schedule their revision. Or to schedule when you will set exam questions. Or anything else. But I have found it a very visual way to see the idea of spacing, and it is also useful to help explain what it should look like to students.