- Analysis and Approaches Standard Level (AA SL)
- Analysis and Approaches Higher Level (AA HL)
- Applications and Interpretations Standard Level (AI SL)
- Applications and Interpretations Higher Level (AI HL)
|
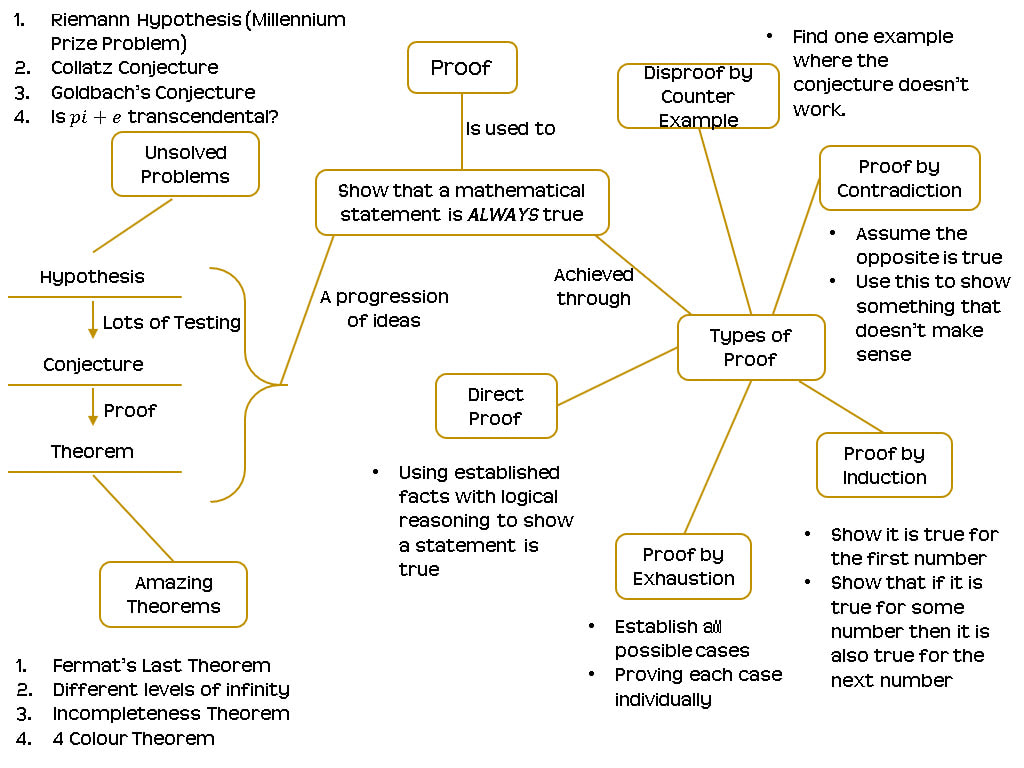
Next week we have our taster lessons for the new IB cohort. The IB syllabus has changed this year, and there are now four options that students can choose from. I will be teaching the AA SL course next year, and for the taster classes we wanted to choose a topic that would show the difference between the courses. We (well I wasn't actually in the meeting, but I agree) chose to use proof. This will make good use of algebra skills, ensuring students know this is a pre-requisite for this course, but also gets to the heart of Mathematics. In preparing for this I have put together a couple of documents. First is this learning map which shows an overview of proof as a topic. They will only need to do Direct Proof and Disproof by Counter Example in the AA SL course (though Induction and Contradiction are in AA HL), but I think giving them a broader picture is important. I will reveal this a step at a time, as the powerpoint builds up slide by slide (something like in the gif below). I also put together a lesson sheet for the topic. I have talked before about how I have started using lesson sheets in IB and booklets in IGCSE. This lesson sheet includes examples and plenty of your turns for the students to have a go at, to test their skills in proof. We will see how the lessons go next week, and I will post an update.
1 Comment
I recently read the excellent Making Every Maths Lesson Count by Emma McCrea. Like the original, it is an engaging read, but I really liked the subject specific ideas that this version had to offer over the original. In this post I am going to identify 1 idea from each chapter that I am going to work on over the next year or so. 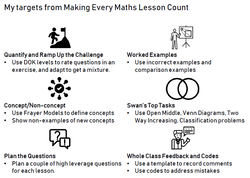 In part 1 of this series I discussed why I have been won over by the humble booklet. In this post I am going to expand on how I design my booklets and what I include in them. I will include images from some of the booklets in the post, but I am not able to share whole booklets as I use some material that I do not have permission to share. I will reference to the main sources I use for each section of the booklet, and give some images of the types of resources used. You can find one full example on Coordinate Geometry here. The front page is fairly simple, with the unit number and title, a space for students to write their name, and the video numbers linked to the topic on www.corbettmaths.com. I also have a back page to all the booklets which has references to websites I use to put them together. Within the unit I start by breaking down the objectives into individual skills that students will need to master. So, for example, in the advanced trigonometry unit there is a skill for sine rule, one for cosine rule and one for identifying which one to use. Within each skill I will break them down into smaller sub skills if necessary. So sine rule is broken down into finding missing lengths and finding missing angles. So the final break down of skills and sub skills for the advanced trigonometry unit is:
With each skill identified, I go about planning them following the same format. Required Prior Knowledge The skill starts with a short item on the required prior knowledge for that particular skill. Sometimes this is a recap of a prior skill from the current unit (eg factorising quadratics before solving them). Sometimes it is something from an earlier unit (eg solving equations before sine rule). As can be seen in the examples below, these take a variety of forms. Some are simply questions on processes that need to be secure. Some are ideas that will lead into the current skill. One of the things I need to work on is developing these to cover ALL the prerequisite knowledge and skills that have not been covered already in the current unit. The point of this section is to help me and students identify if they can do the necessary skills required to do the new skill. If they can't do them, then the lesson will adapt to address those issues first, before moving on with the new skill. There is little point in teaching students to solve the Sine Rule, if they cannot solve equations with the unknown as part of a fraction. It is worth noting here that these are not meant to be lesson starters. I use a retrieval starter of Last Lesson, Last Unit, Further Back as the 'Do Now'. In single periods I have started doing a single retrieval question rather than four, usually from last lesson. I do sometimes plan the Further Back question to address any required prior knowledge too, but this might be a couple of lessons ahead of teaching what requires it. Notes Next there is a section for notes. In terms of teaching, this is when I will explain the new skill, and give any definitions, etc. The notes section is structured as a fill in the gaps exercise, usually with a sentence starter given, and then some space. I also have prepared powerpoint files to go alongside the booklets (though I have stopped using them as much) which line up with the notes section. I now prefer to say and explain the idea and give students time to fill in the gaps themselves. I have been thinking a lot about the use of non-examples at this point of the booklet, and although they are not embedded in them at the moment, I will be adding space for these in the next iteration of them. I am thinking of adding Frayer Diagram templates as well as a way to structure students notes on the definition, characteristics and examples and non-examples of concepts. I have used these a little at the end of units as a reflection activity, but I think they have potential to form part of the actual notes students produce as well, and would push me to think more deeply about non-examples. Example Problem Pairs The notes section is followed by sets of Example Problem Pairs. These largely follow the idea set out by Craig Barton here, though I have not been so careful with making them minimally different yet. Perhaps I will adjust these moving forward. Printed are both the example and the your turn problem, as you can see below. This allows me to give students the questions (no time spent copying out questions), and include any images so they don't need to draw them. It also allows me to include graph paper when necessary, along with any other diagrams (for example they can write straight on transformation examples). Of course this does introduce the potential issue of students rushing ahead and not paying attention to the example (I will discuss how I deal with this in Part 3). The biggest issue I have found with this layout is that I need to make sure I include enough space for students to write their answers! They tend to require a lot more space than I do to answer a question (bigger handwriting is one problem, but also the fact they are novices so can't "see" the way forward as easily and so jot things around a bit more). This is one of the things I take note of when annotating my copy of the booklet for adapting the following year. I have also just finished reading the excellent Making Every Maths Lesson Count by Emma McCrea, and recently listened to the Mr Barton Maths Podcast with Michael Pershan, both of which mention Algebra by Example. In particular they mention the use of incorrect examples, and this is something I want to explore further within the booklets. Getting students to review an incorrect example, or compare an incorrect with a correct example, sounds like a great way to get them thinking about the details a little more. There is also incomplete examples, where students have to fill in the missing bits, as you gradually reduce the amount that is given to them. Booklets would be great for this as you can have them all printed a ready for students to write on. The number of example problem pairs will vary depending on the skill. For example, in using the sine rule to find lengths, there is a single example problem pair. But in graphing regions using inequalities there are a total of 8 example problem pairs. These are included to go through the different variations of the types of questions that can occur. If a class is moving on fine though, I might push them to do the remaining examples themselves, rather than working through them. Exercise After the example problem pairs, there will be an exercise. This will probably be a fairly classic set of questions to practice the new skill they have just learned. I do sometimes make use of the sets of questions from Variation Theory, but also use CorbettMaths, Dr Frost Maths, 10 Ticks, exercises from our ebooks, Pixi Maths and my own site Interactive Maths. These are not the only ones I use, as I also get stuff from TES and Resourceaholic, and have found the old textbooks great for some of these too. I like to include more than enough practice in here for students to do, so will generally have much more than I need. This is also the bit of the booklet where students write in their own exercise books to save space, so I can bunch questions up as much as possible. This allows me to choose what I want them to do based on how they are understanding the material. For each skill there is also an accompanying powerpoint that has the answers to most of the exercises. Further Practice Sometimes I will also include links to even further practice for students. Usually this is to a page in their textbook or CorbettMaths, but also CIMT. We very rarely use these in class, and they are provided as extra for students to do in their revision outside of class. Test Your Understanding? These are not always included in the skill, but when they are I use them as a quick way to check before moving on to another subskill, or before more independent practice. These will usually be answered on mini-whiteboards, and are there in case students struggled with the your turn and need a little more guided practice before moving on to the exercise. They normally include 4 questions similar in style to the example problem pair. Sometimes instead of including these in the booklets, I have used diagnostic questions as part of the powerpoint, which I project and students answer by raising the number of fingers that correspond to the answer they think is correct. Another sub-skill? Sometimes a skill is broken into smaller sub-skills. Rather than creating booklets with 20 skills for a unit (which I feel can be a bit overwhelming) I will not relabel these sub-skills, but rather incorporate them into the bigger skill. For example, in the skill of Sine Rule, there is a section on finding lengths and then on finding angles. I also make a lot of use of these in the first skill of a unit when that is largely prior knowledge. For example, in the unit on Quadratic Equations the first skill covers expanding, factorising and use of the graphical calculator. I do not want to dedicate a whole skill to each, but this does mean there is some material on these if I discover I need to reteach some bits of it. Each new sub-skill will follow largely the same layout as above. I am more likely to use Test for Understanding instead of an exercise if there are lots of sub-skills that build up, and then include the exercise at the end of the whole skill. Activities I sometimes include activities like matching activities, or odd one outs. These will often cover the whole skill and so will be included at the end of the skill. Sometimes this is just a blank space with a title to stick in the cards. Other times there is more structure. It depends on the activity. This is where I still get to include some of the great activities you find on TES. Challenge At the end of the skill there is usually a challenge section. What I mean by challenge is that it is not your "ordinary" style questions. This is where I include things like Maths Venns, stuff from Don Steward, Clumsy Clives, Arithmagons, stuff from nrich, UKMT questions. This is not something I included from the beginning so not all booklets have them yet, but I will be adding as I find new things and adapt them the next time I teach the unit. More so than other sections, this is the one I find most useful to have available at any time, as I can push students who have demonstrated a basic understanding on to these tasks to develop their understanding further. Unit Review At the end of the booklet I like to include a unit review section. This will always include a Unit Review Worksheet which basically has a two questions on each of the sub-skills from the unit. It is meant to be used by students to assess themselves on what they can and cannot do. There are also sometimes activities that cover the whole unit, though these really do depend on the unit in questions. Exam Questions For some units I also included a section of exam questions on the topic at the end of the booklet. We already have a set of documents of exam questions by topic, so this is not something I have done religiously as they already existed. However, I am starting to think that including them at the end would remind me to make use of them more often, and would truly enable students to have everything in one place. Concluding Remarks In part 1 I discussed 10 reasons why I have been won over by the use of booklets. Some of these are determined by the way I make the booklets (e.g. having everything in one place). Although there is definitely an initial time commitment to putting these booklets together in the first place, in following years you only have minor tinkering to do for a whole unit, which allows you to focus on how you can best use the booklet in your teaching, and how you can use that extra time made available to teach better. In part 3 of this series I will be exploring how I go about using the booklets I produce, both in planning and in class. Do you use booklets in your teaching? What do you include in them? Do you do things differently to me? If you don't currently use booklets, could you see any benefits in having a resource like this?
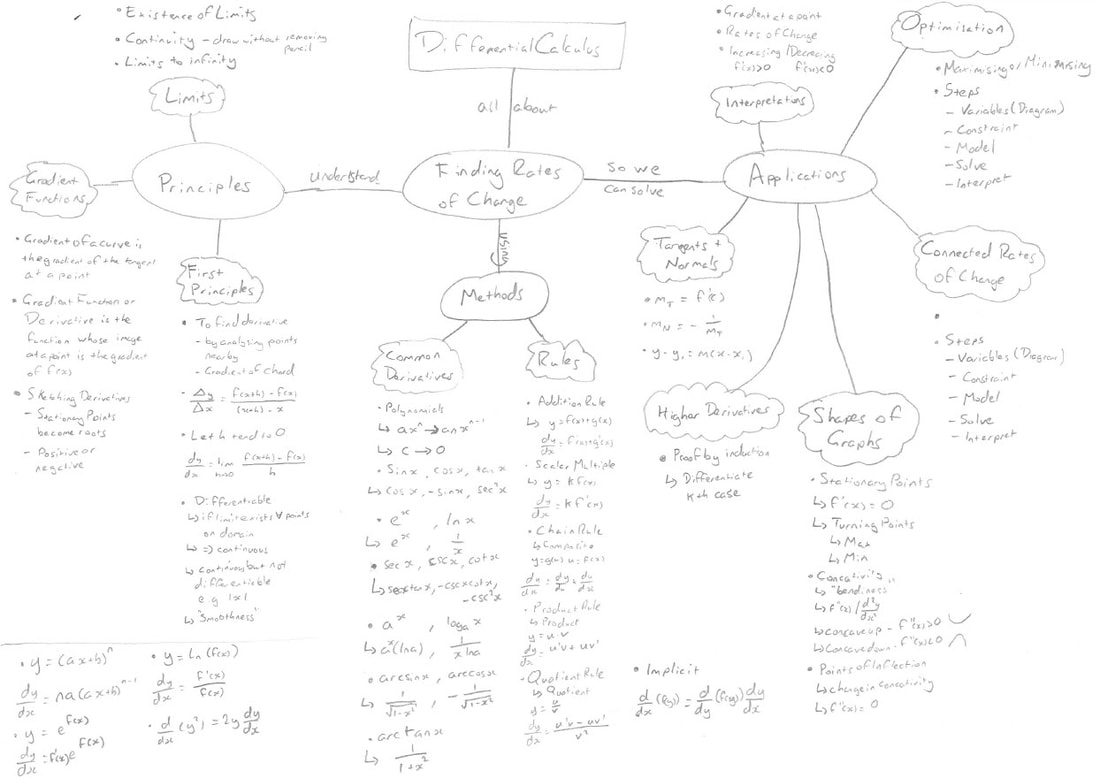
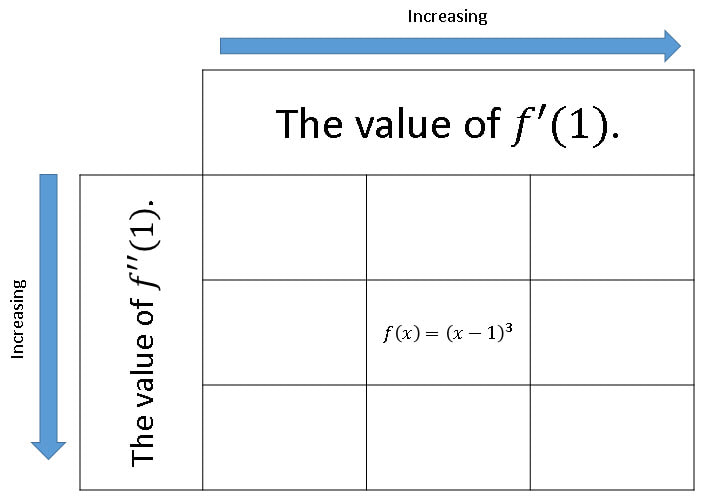
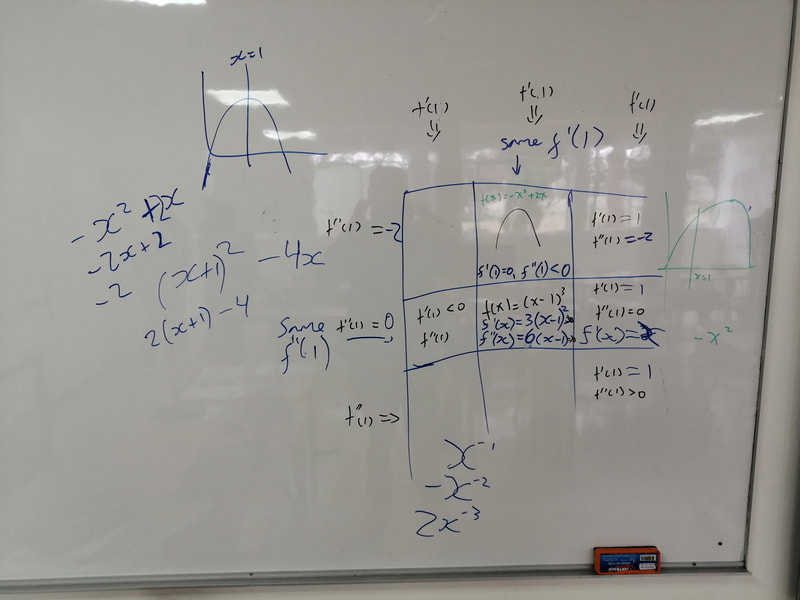
Learning Map In High Impact Instruction, Jim Knight talks about what he calls Learning Maps. These are designed by the teacher to show the learning of a given unit, but also emphasise connections. The completed Learning Map is a revision resource for students, but also lends focus to lessons. He suggests starting lessons by referring to where you are on the map, and finishing by updating the map with what you have learned that lesson. As well as being a tool for in the classroom, I particularly like the way they can help me plan out a unit. So I decided to give them a go in the recent unit I taught on Differentiation to my IB HL class. ll as being a tool for in the classroom, I particularly like the way they c Before planning the unit I started by drawing up a rough version of a map that showed all the things they needed to learn, grouped under some headings. With this, I started planning the Lesson Sheets for the unit, working my way through the objectives listed on the rough map. Once the sheets were finished I then drew a neat finished map, with more details rather than just headings. The point was that all things covered would be on the map. To start the unit we drew the outline, with just the headings. I did this under my visualiser and students made their own version. As we went through this I summarised the key points verbally. Anecdotally, I felt that this gave them a big picture of the unit. It allowed them to see what we were going to be doing, and where we were going. Given that many in the class had done Additional Maths at IGCSE, they had already seen the basics of differentiation, so giving this big picture showed them there was a lot more to it than in Add Maths! Then, every few lessons, we would take out the map and add to it the details of what they had learned. This included key points and definitions. As the unit progressed, the map grew in detail, and became more like my version. Of course, there were a few things that I missed off my version of the map (using induction with differentials, some common derivatives) that we actually did talk about in class, and we added these to the map too. If I missed something off that I had mentioned in class, students were quick to say it. Often these were things said in passing, that I hadn’t planned, but next time I will know to plan them more specifically into my lessons. The end result is shown below (and available as PDF here). The students said it was a useful exercise to see the topic grow organically, and also liked the fact that they had a one page summary revision sheet. One student commented on how she was a little scared at the start as the map was so big, but that filling it in helped her realise the connections between the different things we looked at. Overall I was pleased with this first attempt, and I will continue to use them with this class. I am not sure if I will start referring to it every class as Jim Knight suggests, but we shall see. Differentiation Increasing Activity After listening to the Mr Barton podcast with Chris McGrane, I have been thinking more about task design. I really like OpenMiddle problems, and MathsVenns. But the More/Same/Less idea is one I have not used much. After trying a logs one from OpenMiddle, I decided to give making one a go for my IB HL class. The activity created some excellent discussion amongst students, with them arguing with each other about answers. One girl took the particularly interesting route of sketching what each must look like, before finding functions that would work. Most of the groups missed the fact that boxes beneath each other can't just have f'(1) less than 0, but that all three boxes needed to be equal, but perhaps that is a less important part of the process, as they all thought hard about how to input functions in the right places. I am becoming a big fan of this type of activity, and will try to build them into my teaching more often. IGCSE Booklets Part 1 I posted the first of a three part series on using booklets with my IGCSE classes. This first post looks at 10 reasons why I love booklets. Ingredients for Great Teaching
I wrote a summary blog post of this excellent book for my school T&L Blog. Over the last couple of years I have moved to a booklet model of teaching my IGCSE classes. In other posts I will detail how I put together a booklet and how I plan lessons using a booklet. But in this post I want to start by exploring what I mean by a booklet and why I decided to move towards using them, and why I am now won over by their usefulness. I design booklets for each unit. They cover the different skills within a unit, building up to exam style questions. A booklet is designed to contain all the resources I might need whilst teaching that particular topic. That does not mean I will use everything in the booklet, but that I do have a variety of things available to choose from. Depending on the class, I will adjust what I use. So why do I use booklets? Here are some of the reasons I have come to really appreciate them. It forces me to think about the whole unit (or learning episode) The first huge benefit is that it forces me to consider the whole unit when planning, not just focusing on lessons. There has been a lot of talk recently about the lesson being the wrong unit of time to plan for, but when our time is split in that way, I find it difficult to not plan in those chunks. Using booklets has helped me break through that barrier. In creating the booklet I have to do it before I start teaching the unit so I can give the complete booklet to students when we start. This means I have to think about all the individual skills that form a part of the unit, and how they connect to each other and build up to the big picture. It means I have to consider not just the order in which I will teach these skills, but how I am going to link them together. Rather than teaching a series of 10 lessons, I now teach the unit. Of course I plan what will go in each lesson, but this is really flexible as we can just pick up from where we finished last lesson. So if we get through it quicker than expected, we can move on, and if it takes a bit longer, there is no need to rush at the end of the lesson. Initial time input but saves time in the long run Putting the booklets together in the first place takes a long time. But now I have a set of booklets on 21 units covering the IGCSE, and I can reuse them again and again. In reality, I make adjustments each year, but the bulk of the work is done. In future I can plan a whole unit in about an hour as I just need to review the notes I made the last time I taught it, and make the necessary changes. I can plan for interleaving and Retrieval of linked prior knowledge more easily When planning lesson to lesson I always found that my focus was on the current bit of new learning, and rarely did I think about interleaving other topics in. But with a bigger picture of planning, I can add more interleaved exercises within the booklet. I don't currently do this, but you could also pre-plan retrieval of prior topics within the booklets. You could design an optimal spacing schedule and plan in these retrieval opportunities within other units. No running for last minute photocopies As everything is in the booklet and the booklet is printed for the start of the unit, there is no need to be running trying to get the worksheet copied just before the lesson. It is also cheaper on photocopying as I am not copying things that I end up not using, and there is little wasted white space within the booklet. Three separate worksheets might fit on a single double sided page, instead of 3 single sided sheets. Changed focus on lesson planning from finding activities to thinking about explanations, what I will use, how I can supplement In the run up to a particular skill, I no longer have to spend time finding/putting together a lesson/activity to use. I can focus my attention on thinking about how I will explain difficult concepts clearly, what visualisations I could use to enhance my explanations, and any other materials that might enhance the teaching of that particular skill. I don't forget any skills Perhaps not groundbreaking, but I can't forget to teach something. It is all there and in my face. I can't get to the end of the booklet without teaching everything from it. Of course, I could forget to include something in the booklet, though that is less likely. What does happen is that I realise I need to break a skill into more smaller bits, but I can just take a note in my copy of the booklet to refer to later. Constantly improving And on that note, whilst teaching I can easily annotate my copy of the booklet. This means I can note anything that doesn't work, or works particularly well, as a reminder for next year. As some of my colleagues are also using the booklets, my hope is that they will start making suggestions too and the booklets will continue to improve each time they are used. No need to reinvent the wheel each year. And because I don't need to focus on creating the whole thing each year, I can give my attention to finding/creating more interesting problems. This year, for example, I have tried to put more Open Middle and Maths Venns problems into the booklets. Everything in one place means it is more efficient to navigate to content in lessons - means I can be more responsive in my teaching With everything in the booklet it is easy to navigate as I just say the page number they need to turn to. No getting out different books, or finding the ebook. For most things they don't even need their exercise book as they can write straight in the booklet. This saves maybe 3-5 minutes every lesson, which over a few weeks really adds up. The other advantage to having everything in one place is that I can be more responsive in the way I teach. If students need more practice, there is loads in the booklet so we can just carry on with that. If some students need to be pushed a little harder, there is a challenge question (available for all students, not just the 'high achievers'). If the whole class is ready to move on within a lesson, that's fine, we can just move to the next skill. No filling time as I don't have resources prepared. Standardise the format In Teach Like a Champion 2.0, Doug Lemov discusses the strategy he calls Standardize the Format. The idea is that I can save time and effort checking student work if they all answer in the same format. Booklets are perfect for this as they guarantee that all students will write in the same space. Walking around the classroom you can quickly look to see every response, as they are all in the same space, so you don't need to hunt for them. Students can use them for revision My students have been particularly happy with the booklets in the run up to exams. The booklet gives them a structure to their notes, clearly shows examples, and has plenty of practice questions for them to do. I provide an electronic blank version of the booklet too, so some students use this in their revision, printing it off and filling in the examples and your turns again. What a great way for them to practise the skills they need. So there are 10 reasons I have grown to love the booklet. Many of these relate to workload issues, and many more relate to better teaching. I feel that by using booklets I have been able to focus more on my teaching (explanations, examples, models) and less on the activities. Moving towards using booklets has happened alongside my general switch to a more explicit teaching methodology. I love them. And my students are also overwhelmingly in favour of them. In the next post I will be looking at how I actually go about making a booklet and what I include in them. Do you teach using booklets? If so what are your reasons for using them? If not, have you ever tried it? Is it something you would be willing to try?
Ben Gordon suggested this idea, and started it off on his "Teach Innovate Reflect" blog. Peter Mattock picked up the mantle in his blog too, as did some others. Ben has collated the posts here. I am going to use the same format that Ben suggested, which can be seen below: Format:
I have grown to think it is really important that we seriously reflect on what we do and why over the last few years, as well as thinking hard about what we read and the implications it has on our teaching. This is why I have been doing semi-regular Personal Reflections posts. I am planning on building in some dedicated T&L time later in our year (southern hemisphere, so we are only a third of the way into our year) for staff to quietly reflect on their targets and how they have progressed towards them. But it is also important for teachers to take control of their own professional development, and writing blogs has always been that for me. So here are my High Five for this year (well actually a High 7, but I hope you will indulge me!) 1. MARGE What I learnt: The stages of learning that we as teachers need to be aware of consist of Motivate, Attend, Relate, Generate, Evaluate. Source: Arthur Shimamura's paper MARGE; found through Tom Sherrington's blog post. Implications: When planning a sequence of learning we need to build in opportunities for students to partake in all five aspects of learning. We should help students to MOTIVATE their minds so they are primed for learning. The use of creating curiosity was a big take away for me, as well as building in anecdotes and stories. Getting students to ATTEND to their new learning is really important (Willingham's "memory is the residue of thought") and we often have to direct students attention to the important aspects as they are unable to do this themselves as novices. Students should have lots of opportunities to RELATE what they are learning to what they already know, with Shimamura recommending the 3Cs (Categorize, Compare, Contrast) and using graphical organisers. We need to give students lots of opportunities to GENERATE their new knowledge (also known as retrieval practice) to strengthen the connections. And finally we should allow students to EVALUATE their learning (this seems to be linked to metacognition to me), especially after some time has elapsed (to check for learning not performance). I find this acronym useful to bear in mind when planning a learning sequence, so I can try to ensure I give students opportunities to do each of these things. The ones I have recently been incorporating a lot more of are GENERATION through weekly quizzes and Last Lesson, Last Unit, Further Back reviews at the start of lessons, and I use Example Problem pairs to help students ATTEND to what they need to. In the next bit I share one way how I might try to help students RELATE more. I did an INSET session on MARGE and you can find the presentation here and I also compared the model to the EBC model I was introduced to on a Future Learn course. 2. Sequencing Examples and Non-examples What I learnt: The sequence of examples we give can help students construct their own meaning, and so providing a faultless communication through examples can help ALL students succeed. Source: The Theory of Instruction by Siegfried Engelmann; www.variationtheory.com Implications: Direct Instruction (and scripted lessons) is something of a taboo subject in many education circles. After reading The Components of Direct Instruction, I decided to start reading The Theory of Instruction to get a better picture of what it really entails. I am about a third of the way through it at this point, and so far we have been looking at (in incredible granular detail) how examples can help students to understand new ideas. The idea of juxtaposing minimally different examples to highlight what effect variables have seems sensible. But the biggest takeaway for me has been the importance of non-examples of concepts. I need to think hard about how this fits in to a whole host of mathematical ideas. I can see how it works with simple concepts such as definitions, but I am still not sure about more abstract ideas such as processes we follow. I am planning to think about making some sets of non-examples (hopefully in conjunction with my team) for some of the concepts we introduce, as well as making use of https://nonexamples.com/ and trying to incorporate the use Frayer Models more regularly (I suggest some Thinking Activities here). 3. The four phase model of learning a skill What I learnt: When learning new ideas and concepts we go through a four stage model of Teach, Do, Practise, Behave. Source: Mark McCourt: The Return on the MrBartonMaths Podcast Implications: Since we all go through these phases when learning, it is of interest to me both as a teacher and as the person running the CPD programme at my school. As Mark states in the podcast, most lessons only cover the Teach and Do phases, as this shows performance ability. Of course, these are vital steps in the journey. But I have found that I am not incorporating as much independent practice into my classes as I would like. Or maybe I am? I do retrieval starters (though Mark would not like these as they break up the learning episode), and weekly quizzes. This cover topics in a mixed order, but do not focus on a particular skill. I think I need to build in more time for intelligently designed sequences of questions on a topic. I am making a bigger effort to include ideas from the behave phase at an appropriate time (Mark suggests 2 years after initial teaching), and I do this mainly through the weekly quizzes and the Further Back questions in my starters. These are usually out of context exam questions. But perhaps I need to build in more problem solving questions from the likes of NRICH and UKMT. And what about CPD? Teachers need to go through these phases too when improving their practice. We know that one off sessions don't lead to improvements (though they might be a useful starting point). But most CPD only utilises the Teach phase. No chance for teachers to Do. When running sessions I will endeavour to build in more opportunities for teachers to actually Do the strategy in a role playing environment. But the real power of this model will be in the coaching programme (discussed below). 4. The importance of sleep What I learnt: Sleep affects so many aspects of our lives and wellbeing. In particular, sleep is an essential part in the learning process where new ideas are consolidated. Source: Why We Sleep by Matthew Walker and Learning How To Learn MOOC. Implications: Many students do not sleep enough (e.g. here). It is so easy for them to become distracted that sleep seems like something that can be pushed aside. Many of our students claim the workload of the IB means they have to choose between working and sleep (so they choose to work). Of course, whilst there are high demands in the IB, this is not true. It is all the other things that take up time they should be getting rid of. The myth of multitasking probably leads many of them to being less efficient than they could be. But maybe if they knew the damaging effect that lack of sleep can have on them, they would take it more seriously. Increased risk of heart disease, cancer, car crashes, anxiety, depression, and a host of others. We need to start educating students in the importance of sleep for healthy lives. We talk about diet and exercise. But rarely is the importance of sleep discussed. And from a teachers perspective, I need to be aware that this lack of sleep might be playing havoc with what students remember from day to day. If they are not getting enough sleep, they are probably not consolidating the new learning effectively. However, whereas accepting that students will forget between lessons due to the forgetting curve can help us teach better (as we can incorporate spaced retrieval, for example), we should not accept that lack of sleep is the way it is. Whilst not being surprised by it, I will still try to educate the students to make sleep a priority in their lives. 5. Instructional Coaching is an effective form of professional development What I learnt: there are different forms of coaching and instructional coaching is placed well to lead to improvements in teaching. Source: The Impact Cycle and the Instructional Coaches Institute. Implications: Instructional Coaching positions coach and teacher as partners (in accordance with the partnership principles). Whilst the teacher is the decision maker about their goals and what they will do, the coach enters a dialogue with them to help find a way forward. As this is a dialogue, the coach will offer suggestions and support (different from a facilitative model), but will not force their methods upon the teacher (different from a directive model). The benefits of coaching are that it is sustained over a period of time and individualised. Each teacher gets support in the area they want to focus on, and coach and teacher work together until the teacher is successful. The sustained nature also allows teachers to not just go through the Teach phase, but also the Do phase (practising before using it in class) and the Practice phase (as they use it in different contexts over a few weeks). The behave phase will come later, after the coaching cycle has finished, but this puts teachers on the path to success. 6. Think of the introverts What I learnt: Between a third and a half of people are introverts, but many of our school systems are built for extroverts. Source: Quiet by Susan Cain Implications: I am an introvert. I have started reading this book, and it has already had some profound impacts on me. Introverts react differently to stimulation than extroverts. They actually are more receptive to stimulation (from social stimulation, to caffeine stimulation). Which means they require less of it. Indeed, they are much more easily over stimulated than extroverts, who need more stimulation to stop them from becoming under stimulated and bored. This is something I experience daily. When in a group of people I literally cannot focus if more than one conversation is going on. I am being over-stimulated by the multiple conversations. And it is tiring. It is not that I don't enjoy these conversations. In fact, the ones that give me something to think about are great. But afterwards I need some time to decompress. Much of the world today, including schools, is designed for extroverts. But many of the greatest inventions and discoveries through history came from introverts working in solitude (Newton and Gravity, Wozniak and Apple computers). They are the often over looked leaders (the introverted Rosa Parks compared to the extroverted Martin Luther King Jr). A few things come to mind: 1) how can we utilise the power of the introverts in our classrooms, both as individual thinkers and leaders? And how can I ensure that all students can benefit from the power of thinking deeply (links back to the independent practice from above). 2) how can we ensure we are not over stimulating introverts, and giving them the time they need to decompress? If they are always in environments where they are expected to work in groups, or there is lots of chatter going on, they will become exhausted (and probably not aware of why). 3) how can I as an introvert be more aware of my own personality, and use this to my advantage. 4) Don't use phrases like "He needs to be more active in class" in reports. For introverts, that is just not how they learn. They work by thinking hard to themselves, unlike extroverts who think openly and require input from others. Saying things like this just perpetuates the myth that we should all aim to be extroverted. 7. The Power of Cold Call and Show Call
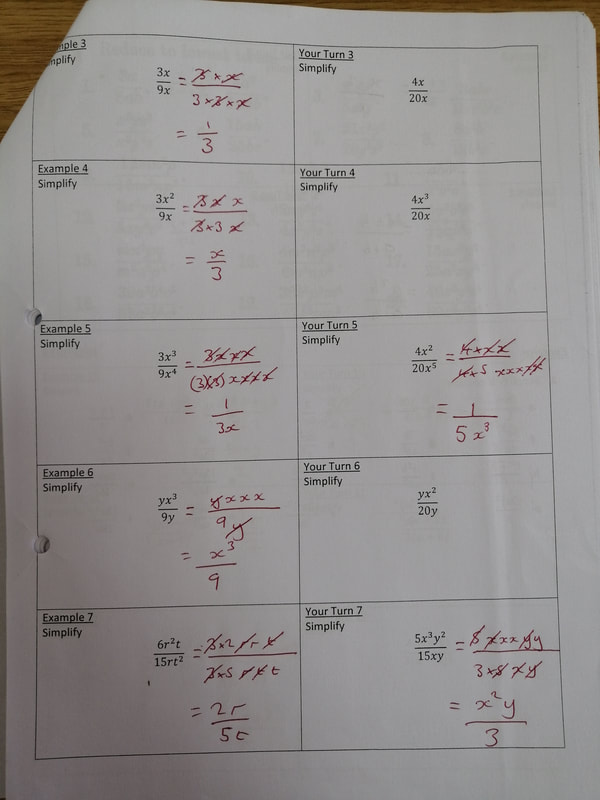
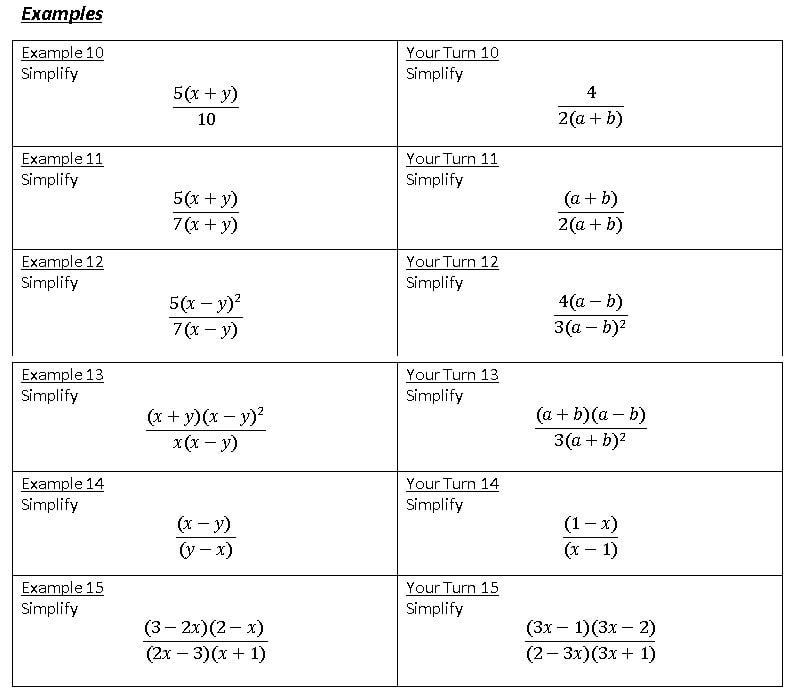
What I learnt: Cold Call and Show Call are excellent ways to check for understanding and build a culture of accountability in class. Source: Teach Like a Champion 2.0 by Doug Lemov Implications: This book is a must read for all teachers. It is full of strategies that we can all use in our classes to enhance the learning of our students. But it was Cold Call and Show Call that had the biggest impact on me. By using Cold Call I have students not only answering the questions more regularly (as they know they could be asked) but also I benefit from a better understanding of what they can each do at any point in time, and they benefit from hearing explanations as to why and how things work from their peers more often. Similarly, with Show Call, I can show students work to the whole class. I do this using a visualiser (my favourite bit of kit at the moment). We can dissect errors and misconceptions. I can show off exemplary work. I have been teaching algebraic fractions to my S4 IGCSE class. I am about halfway through the unit, and I wanted to take some time to reflect on how it was going so far. I started the unit by getting students to answer a serious of questions on cancelling fractions and equivalent fractions. I generated these using my website as I wasn't concerned about the order of questions as it was all stuff they had done before. However, in reviewing this, I decided to talk explicitly about what we are doing when simplifying a fraction. I was very deliberate with my wording "We are looking for common factors in the numerator and denominator that we can cancel". In saying this I broke the numerator and denominator into a product of factors, as shown below. We then extended this, with me saying "To simplify algebraic fractions we find common factors in the numerator and denominator which we can cancel." Following this I ran through a series of Example Problem Pairs (shown below). I have started doing this using my visualiser so students can see the layout I use in the booklet they have to copy the examples into. I broke up the numerators and denominators into the factors, then cancelled them (I have always taught spotting these before). There are 9 example problem pairs, showing different types of simplifications they may come across. As this was quite a lot of examples, I didn't want to spend ages going through them all, so I decided to do it quickly. For each example, I called students attention to the board ("Eyes on the board" - I have been working with them for 6 months on how to behave during examples, so this is all that is needed most times), and then I worked the example on my copy of the booklet. They are watching the screen, not talking and not writing. In this case I did not feel the need to narrate after doing the example. As soon as I was finished I said "Your Turn", and all students copied down the example and attempted the corresponding problem. I then Cold Called a student to give the answer to the Your Turn, making an effort to congratulate them for getting it right. In one instance the student wasn't sure, so I asked them to tell me the first step, which I wrote down in the Your Turn box (Your Turn 5), and they finished the explanation by themselves without further prompting. I then sent students to my big whiteboards that I have around my room to work in pairs answering the following set of questions from the textbook. After a few minutes, they had all made really good progress (much better than when I have them work at their desks). During this time I had been able to quickly see the work of every student as they were all on display to the whole class. This was followed by another quickfire round of example problem pairs, where there were factors in brackets. I made a big deal to refer to them as factors throughout. Then back on the whiteboards for some more practice. I followed this same pattern through simplifying algebraic fractions that needed to be factorised first, and here is where my over emphasis on the need for factors paid off. Another set of example problem pairs on linear expressions, with time on the boards, and then quadratic expressions. Students spent 25 minutes working individually in their books on the questions for these, as I explained to them that they were more difficult and they would need to give it their full attention. For a class that are generally quite chatty, they worked pretty much in silence for 20 straight minutes on difficult algebra problems. I was in shock (in a good way!) I did make one error here when addressing prior knowledge. Although I got them to factorise a few quadratics so I could check if they were OK with this, I obviously didn't give them enough time on it, especially those with a coefficient of x2 which was not 1. This ended up distracting from the simplifying fractions, and I decided to ask them to skip a few questions to focus on the skill we were looking at today. I need to come back to reviewing more complicated quadratic expressions, and build in some algebraic fractions too. The following lesson we moved on to multiplying and dividing algebraic fractions, and followed a similar process, though with only 2 example problem pairs (they didn’t need any more by this point). I also started this lesson with a set of questions on multiplying and dividing numeric fractions, and showed the class how to cross cancel before performing the operations (which some had never seen). I then had them work on a challenging exercise from one of the old textbooks recommeded by Jo Morgan at Resourceaholic. I particularly liked question 10, and once we had found the answer, I was even more convinced of the beauty of this expression. I explained to the class why it was beautiful, and challenged them in the last 5 minutes to create their own beautiful expression that simplified down to an integer. I have now got to teach adding and subtracting algebraic fractions, and then dealing with complicated equations with algebraic fractions too. I am going to try to follow a similar process throughout the rest of the unit. I have found the quickfire example problem pairs to be a great way to keep my lesson moving at a good pace, as I have found in the past that these can really slow the lesson down. Although sometimes that extra time is really needed to dig deep into the example and details, in this case, I think seeing lots of different examples close to each other allowed my students to make connections for themselves. All students were able to perform in the lesson, fully able to deal with all the stuff we have covered so far. I am happy that I have laid a groundwork of success for the students before we now move into the slightly more tricky bits of the unit. Hopefully that feeling of success will run through, and students will continue to believe they can do it. I know that them performing in the lesson is not a good indicator of their long term learning (these will be cropping up in starters and quizzes over the next few weeks and months to guarantee that), but I have never taught algebraic fractions before when all students left the room able to do it (except when I have taught the top set Additional Maths class). And this is definitely a good step in the right direction. After each of the lessons in this sequence I left the class feeling like ALL my students knew more than when they entered my classroom. On top of this, ALL the students were working for the full 40 minute period, fully engaged by both the quick pace of the example problem pairs and the use of the whiteboards for answering questions. Overall, this is definitely something I am going to build into my teaching on a more regular basis.
New School Year We have just started our new school year in Peru, and the kids have been back for a week, after an INSET and Preparation week. It has been tough to get back into the routine, but it doesn't take long to get back in the habit. In the INSET week I launched our new Principles of Great Teaching document with two sessions with our staff: introducing the document in general and then focusing on the first standard, which is having an activity for students to do as they enter the classroom (inspired by Doug Lemov's Do Now). It has been accepted well by colleagues, who have commented on it being useful to track their own development, and as a guide towards great teaching. Most people were even on board with the Do Now, though we will have to see how that goes as term progresses. In general, people were very positive about the whole week, and I have had a couple of comments about it being more useful this year than usual, even though staff had less time to prepare for their classes. My personal focuses for this year that are taken from the Principles are:
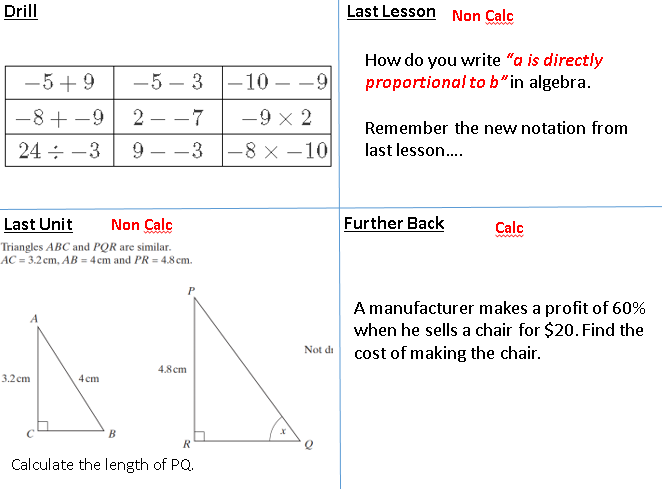
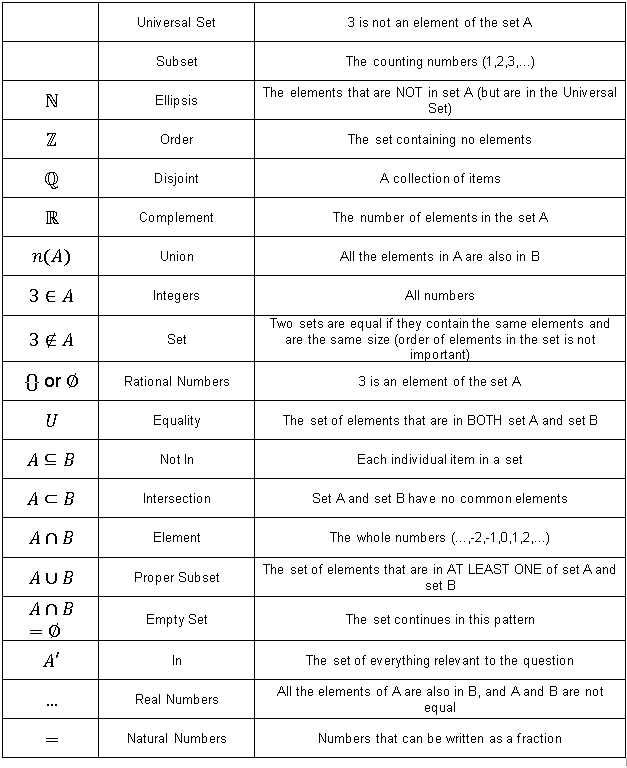
In terms of teaching, I have started my classes with more clarity on my expectations for lessons with me, by producing this document which I have on my walls, and have given copies to my students. Introducing Direct Variation with S4 In the first lesson of the year I introduced my S4 class (taking IGCSE this year) to the concept of two variables being connected by a constant factor, and linked this to previous work on proportion. I ended by showing them the notation for a is directly proportional to b. We continued this work in the double on Tuesday. I started with the traditional Last Lesson, Last Unit, Further Back, but I have added a new section this year: Drill. The idea is to drill some of the most basic skills so they do not occupy space in working memory when solving more complex problems. After reviewing a couple of bits from this, I moved on to a silent example problem pair. I used Show Call on the Your Turn problem, choosing a couple of pieces of work I noticed while circulating, one using 0.75 and the other using 3/4. Previously I have written the examples on the SMART board, but this year I have decided to do it using the visualiser live on a copy of the booklet I give to students. This worked well as it gave them more guidance on how to lay it out (although I needed more space to keep the vertical structure I would have preferred). I then had students complete a short exercise in pairs on the big whiteboards I have around my room. I much prefer this way of working than using mini-whiteboards, as it is easy for me to see everybody's work, and to draw attention to important points. For example, one pair started with x=ky whereas everybody else started with y=kx. I used this to identify that their values of k were different, but the final answer would be the same. As it was on a big board, it was easy for everybody to see. After a couple of groups had finished the 10 questions, we moved on, and I had the class generate the 5 steps for the process. I insisted on them using proper vocabulary (substitute not "put in"). I followed this with a quick Pepper round (also Lemov), asking them quickfire questions on their squares, cubes and roots. This energised the room nicely before seguing into some more examples-problem pairs, where we have proportional to squares and roots. I actually decided to have students attempt Example 4 by themselves before I showed them, and several got stuck by the fact that it was asking for the value of the subject of the formula. When I then showed them, they had had a chance to think about it, and this step made more sense. Then I used a few Diagnostic Questions to check for understanding of notation and steps. We finished with some independent practice questions taken from Dr Frost. Next lesson we move on to Inverse Proportion. Gratitude I downloaded the 5 Minute Journal App towards the end of the holidays to start developing my own reflective processes. Each day I have to come up with 3 things I am grateful for, 3 things I will do to make the day amazing, and then in the evening reflect on 3 things that were amazing, and 1 thing I could have done to make it even better. I am finding it difficult to come up with new gratitudes each day, but it is slowly becoming easier. I have built it into my morning and evening routine now, so I am remembering to do it. I am starting to feel generally more positive about situations, and I am hoping that this will help me become more charitable in my interpretations of what people say, as well as making me more aware of my own good fortunes. It is very easy to focus on the negatives, and this will hopefully stop me from doing that so much. Team Teaching My colleague and I who are both teaching IB Mathematical Studies, have decided to combine our classes and team teach this year. It is the second year of the course, and we always have a few students leave school at this point (it is only compulsory until 17 in Peru), so we both have small classes (less than 10). We figured this will allow us to provide more support, especially during independent practice. We are going to see how it goes, and I will reflect more on it as we progress, but I am excited to give this a go. Sets Notation Matching We started the new year with a unit on Sets and Probability with the final year IB Mathematical Studies classes. Sets is something they have encountered several times before, and it is on the IGCSE that we do. However, the notation is always something that causes confusion. To start the unit we decided to do a matching activity with the symbols, the names and a brief description. The activity was done in pairs, and there was lots of good discussion and questions about some of the notation and words. They had not seen the words Order, Disjoint or Ellipsis before, so these threw a lot of them, even though they had an idea of what the symbols meant. This gave us a pretty good idea of which were the problem areas (subset vs proper subset).
I have previously blogged about How I Teach and in more depth about my Weekly Quizzes. In this post I am going to go into a little more depth about the way I start my lessons, using what I call Last Lesson, Last Unit, Further Back. This strategy is based on the idea of spaced retrieval practice, which incorporates both the Testing Effect and Spacing Effect, two of the most well documented ideas in the science of learning. The testing effect says that we learn better by forcing ourselves to retrieve knowledge from our long term memory, as opposed to restudying it. The spacing effect tells us that we remember material better if we space out studying out over time, rather than cramming. Both of these ideas are also considered to be desirable difficulties by Bjork in that they make initial performance lower, but long term learning better. One of the important things with spaced retrieval is that it is most effective if done on the verge of forgetting. This is when it has the biggest impact on learning. However, the time taken to get to this point increases with each subsequent retrieval.
Each year, our students go away for a trip that incorporates some activities, service projects, and outdoor education. But these are done in half year groups, so half the year is away Monday, Tuesday, Wednesday and the other half are away Wednesday, Thursday, Friday. When S3 were away in Tambopata, I had two doubles with them, but in each double I only had half the class (and a few from other collapsed classes). In order to make the most of this time, I wanted to do some activities that would get them ready for the next unit we are starting after they got back, which was functions. Students have previously met the idea of functions, function notation and domain and range, and this unit will focus on composite functions and inverse functions. However, it has been a couple of years since they saw them, so I wanted to review the basics before moving on. I started with this activity asking students to write functions given in words as algebraic statements (taken from here - thanks to Jo Morgan for pointing me in the direction of this reference).
|
Dan Rodriguez-Clark
I am a maths teacher looking to share good ideas for use in the classroom, with a current interest in integrating educational research into my practice. Categories
All
Archives
August 2021
|







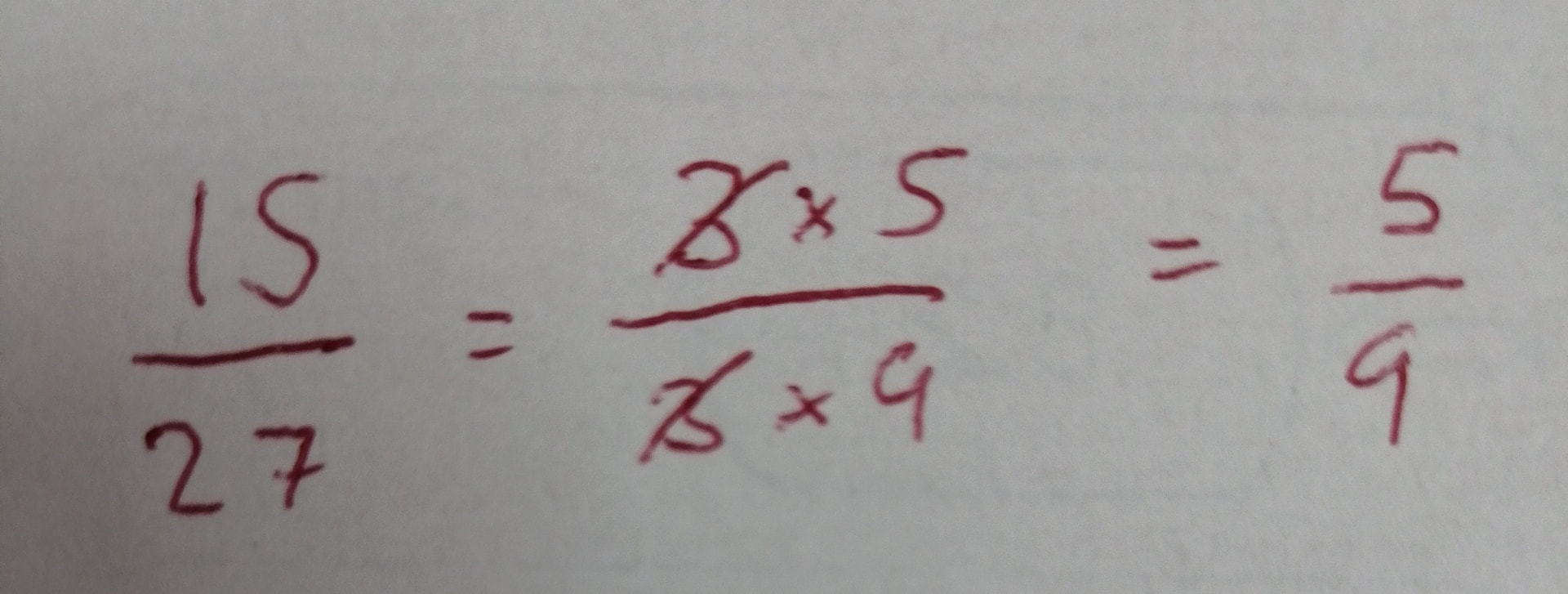

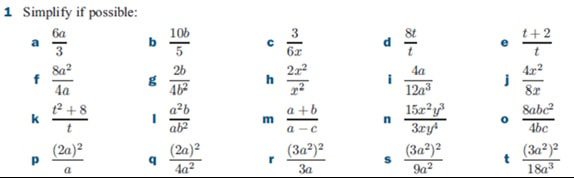







 RSS Feed
RSS Feed
