Planning the unit
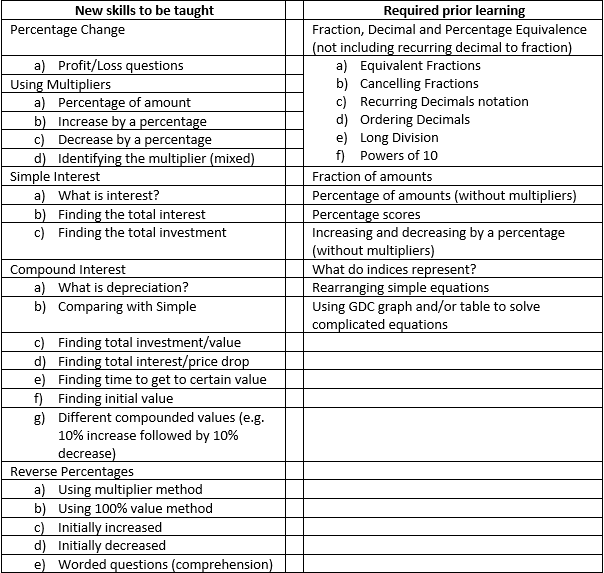
First off, I think it important to acknowledge the bigger picture for any lesson, and begin by planning the unit as a whole. Before anything else, I identify the different objectives I need to explicitly teach, as well as the prior knowledge students should have to be successful in this topic. Identifying all the individual items that will need to be covered in a given unit helps me clarify exactly what it is I need to do, and what I want the students to be able to do by the end of the unit. This is something I have always done, but the process has become much more rigorous since reading this excellent blog post (https://tothereal.wordpress.com/2017/08/12/my-best-planning-part-1/) by Kris Boulton. Below is an example for our first unit of Year 10 on Percentages.
This produces two lists of objectives for student learning: one list of things they should already know; and one list of things I will teach them during this unit. The importance of prior knowledge on learning new content is well established and I have come to believe that checking for prior knowledge and addressing any issues is key to any good instructional sequence. My approach to checking prior knowledge previously has been largely down to asking questions of the class, and perhaps the use of starters in each lesson. Although these certainly served to activate prior existing prior knowledge, they were not always successful in identifying if there was a small problem for some students. I recently read this interesting post (https://misscotterillmaths.wordpress.com/2017/12/24/give-them-a-test/) which discusses in depth the use of Initial Assessments. I really like this idea, and will be using this to start all units this year, giving each class a test in the first lesson which covers the prior knowledge they are expected to know, and some aspects of the new content too. I will include aspects of the new content due to something known as the "pretesting effect" which seems to suggest that testing on unknown content before teaching it can improve later retention after teaching (see http://learninglab.uchicago.edu/Pre-Testing_files/RichlandKornellKao.pdf and https://bjorklab.psych.ucla.edu/wp-content/uploads/sites/13/2016/07/Kornell_Hays_Bjork_2009_JEP-LMC.pdf).
Students will self mark this quiz, and I will quickly check understanding by getting students to raise their hands if they got a question right, and taking a note of how many did for each question on a copy of the unit plan. This will then allow me to plan the following lessons accordingly, if I need to cover any of the prior knowledge material in more depth, or indeed skip over some of the new content they have actually seen before.
Types of Lesson
In developing the learning of students I use two types of lesson: teaching new content; and practicing the skills. I am a firm believer that humans need enough time to practice a certain skill in order to learn it (by which I mean commit it to long term memory), but that they also need very clear instruction when in the initial stages of learning (http://markhamtl.wixsite.com/teaching-learning/single-post/2017/05/24/Why-Minimal-Guidance-Instruction-Does-Not-Work).
Teaching New Content
For each of the objectives I have identified I would separate a time to follow this process. For some this will be no more than 10 minutes, and for others it will run over more than a single period.
Retrieval Starters
Each lesson begins with a retrieval or fluency starter. This is slightly different for different age groups, but they are all designed to last between 5 and 10 minutes.
With Middle School classes, I use a fluency developing programme called Numeracy Ninjas (http://www.numeracyninjas.org/), which is designed to develop their mathematical fluency in the basic skills required for the subject (number bonds, timestables, rounding, etc).
Previously, with IGCSE classes I used a similar set of resources called the Corbett Maths 5-a-day (https://corbettmaths.com/5-a-day/) which covers the basic skills required for IGCSE Maths. However recently I have started to make use of daily retrieval challenge grids (as described here https://lovetoteach87.com/2018/01/12/retrieval-practice-challenge-grids-for-the-classroom/, with links to templates here https://ictevangelist.com/retrieval-practice-challenge-grid-templates/). I do not run them in quite this way, as I want all students to answer all questions rather than choose, but the concept is the same (see below).
These are designed to make the most of the idea of retrieval practice (http://markhamtl.wixsite.com/teaching-learning/single-post/2017/11/07/Retrieval-Practice), and also build in some spaced practice. The important part of these is that they are done individually and without looking up how to do it (thus making use of the strength of retrieval to improve learning). They are always self-marked, and in a similar approach to the initial assessments, I asked students to identify if they got each question correct, which informs my future use of questions.
I spend some time explaining the importance of retrieval with my students in the hope that they will use this opportunity to improve their learning. It has been shown that actively developing student metacognitive strategies can improve learning outcomes significantly (https://educationendowmentfoundation.org.uk/evidence-summaries/teaching-learning-toolkit/meta-cognition-and-self-regulation/).
Introducing New Content
When introducing the new content I will teach it explicitly, mainly using example problem pairs (https://gregashman.wordpress.com/2016/02/09/example-problem-pairs/) where I do one example and then students do a very similar example. These are presented side by side so that students can refer back to the example whilst completing their question, thus lowering the extraneous cognitive load (http://markhamtl.wixsite.com/teaching-learning/single-post/2017/09/25/Cognitive-Load-Theory-Research-that-teachers-really-need-to-understand). I do the example on the board without asking for ideas from the students. Most of the time I will narrate my thoughts as I do the example, though recently I have started to like the idea of the silent example, where students focus all their attention on the example without the split-attention required to listen to me at the same time. I will then go through the important points afterwards. All students are expected to do the second question, and after recently listening to the Mr Barton Podcast with Doug Lemov (http://www.mrbartonmaths.com/blog/doug-lemov-teach-like-a-champion-and-top-tips-for-delivering-training/), I am planning to make use of Show Call, where I will take a photo of a student's work and project it on the board (as I explained in this post http://markhamtl.wixsite.com/teaching-learning/single-post/2017/11/01/A-simple-but-effective-use-for-Google-Docs-in-class), either as an example of an excellent answer or to identify a misconception.
After teaching the content, it is vitally important for me to know if students have successfully acquired the information or skill, and this is where AFL comes into play. I call this section of the lesson "Test Your Understanding" and this will usually entail between 4 and 10 questions (depending on the complexity) where students will answer them one at a time on mini-whiteboards. These questions are designed to check if students have grasped the concept I have been teaching, and are usually similar to the examples presented. Once they have had enough time to answer the question, all students raise their mini-whiteboard, and I pick up on any misconceptions. An alternative option at this stage is to use well designed multiple choice diagnostic questions (https://diagnosticquestions.com/), where each incorrect answer reveals a specific misconception. If using these, I will usually ask students to vote for their chosen answer using 1 finger for A, 2 fingers for B etc. In both cases, students do not answer until I ask them to raise their board, or make their choice, so that they are not persuaded by other members of the class.
During this stage of the lesson I am asking lots of questions to delve into why students have written certain things, and to get students to explain their reasoning. If different students have got different answers, we will discuss this as a class. If I have used a diagnostic question, we will discuss what misconceptions have been made to reach the incorrect answers.
This is the one part of the lesson where I allow students to discuss with the person next to them, which gives them a chance to clarify the ideas in their head, and further develop their understanding. Sometimes I will only give them a single mini-whiteboard between the pair to encourage this dialogue. Through this process I get a pretty good idea of how well the students have understood my explanations, and can intervene if necessary.
Independent Practice
The final part of the lesson entails a small amount of independent practice, where students will do some questions on their own to embed the skill/knowledge they have just learned. This does not necessarily mean a long boring exercise from the textbook (though I have no issue using the textbook). This will usually include some form of purposeful practice, and will be more involved than the test your understanding questions, getting students to apply their new knowledge in some way. One particularly amazing resource I have come across recently which I will be making use of in this part of the lesson is Increasingly Difficult Questions (http://taylorda01.weebly.com/increasingly-difficult-questions.html) where each question is slightly more challenging than the previous.
One of the most important aspects of these lessons for me is that all students can be successful. As I have mentioned before, I am coming to believe that success is one of the biggest motivators for students (http://markhamtl.wixsite.com/teaching-learning/single-post/2017/10/18/Motivation-in-class). This approach has been tweaked over the last two years as I have come to learn about cognitive load theory, and my interpretation is that breaking the learning into small chunks and teaching them explicitly will lead to the best understanding. My recent personal experience backs this up.
Practising the Skills
After teaching the individual skills there is usually a need to put them all together in some way. These lessons are made up of different tasks, such as:
- A simple exercise with questions involving all the different skills. This builds in some interleaving, and as it is a few days after initial teaching, provides another opportunity for simple retrieval. I make use of treasure hunt and tarsia activities quite a lot at this stage. Another popular choice at this stage is doing an exam question relay, where there are 10 questions, and students have to answer one to move on to the next, in a race to be the first to finish.
- A rich task (or low-entry high-ceiling task) which all students can access, but gives plenty of scope for challenge. My go to sites for these types of activities are Don Stewards excellent blog (donsteward.blogspot.com) and nrich (https://nrich.maths.org/).
- A modelling task where students have to apply their new found knowledge to model some situation.
Resources/Class Website
This year I have set up a class website (http://classes.interactive-maths.com/) which contains the objectives for each unit, with links to videos, the pdf versions of lessons and any other resources used in class. The image below shows a unit from the IB Mathematical Studies course.
Last year I started creating work booklets for my IGCSE class. These booklets include everything they need for the unit, including links to revision videos, the notes (with important information left out for them to copy from my explanation) and the examples with space for them to copy the worked solution. Last year I included the Test Your Understanding in the booklet as well, but for next year I am going to remove these, as some students would jump ahead which made it hard for them to fit the purpose described above. I also include either the exercise/activity for independent practice, or the textbook page number, but expect these to be answered in their exercise books.
For an example of the unit on percentages I have just planned see here: https://drive.google.com/drive/folders/1qr5E5iBn_2RuuuS4WVEVrGpmy0oRstJr?usp=sharing
Fortnightly Quizzes
I have read a lot of research on retrieval practice (http://markhamtl.wixsite.com/teaching-learning/single-post/2017/11/07/Retrieval-Practice) lately, and I am starting to believe it is one of the best ways we can help our students achieve their best. Due to this I have started to do fortnightly quizzes covering the topics we have previously covered. Ideally I would do these weekly, but do not feel I have that much time available to set aside. Currently I have only been doing them with my IGCSE classes, but I am thinking of extending this to IB a well.
These run in a very similar way to the initial assessments, in that I take a lesson to administer, self mark and review any areas of weakness. They are zero stakes quizzes, and the students marks do not count towards their grades at all. The questions in these quizzes are usually very knowledge/skills based, and do not require students to apply their knowledge to difficult new ideas. I have read a few blogs recently who approach this in a much more structured way than I currently do, including 2 questions from the current work, 2 from a month ago, 2 from last term and things like this. I like these ideas, and will be building more structure into the way I prepare these retrieval quizzes in the future.
Homework
In the last few years I have used homework as a retrieval strategy, giving a mixed topic homework. However, I have found that these do not work the way they are intended, as students would use their books and hence not actually engage in active retrieval, which is why I have switched to retrieval quizzes in class. This year I will be using homework for independent practice to consolidate key skills. These tasks will be aimed largely at developing fluency in the skill or skills currently being learnt.
Final Comments
I don't think any of these ideas are my own, they have all come from a variety of sources over the last few years. This approach is very different to how I was teaching before I came across the amazing world of education research (mainly through the Mr Barton Podcast http://www.mrbartonmaths.com/podcast/), and I don't know if it will stay like this forever, but I would need a pretty strong argument to convince me that the ideas of CLT and Retrieval Practice were things to drop from my teaching! One of the most influential pieces on my teaching, that I think all teachers should read, is the Principles of Instruction (http://markhamtl.wixsite.com/teaching-learning/single-post/2017/09/11/Principles-of-Instruction) by Barak Rosenshine, and I based a lot of this system of teaching on those ideas.



 RSS Feed
RSS Feed
