Making Every Maths Lesson Count

I recently read the excellent Making Every Maths Lesson Count by Emma McCrea. Like the original, it is an engaging read, but I really liked the subject specific ideas that this version had to offer over the original. In this post I am going to identify 1 idea from each chapter that I am going to work on over the next year or so.

---

Quantify and Ramp Up the Challenge
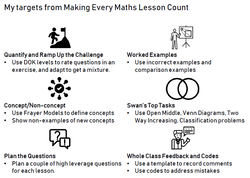
I am interested in the level of question I use in exercises I set. Over the last couple of years I have focused on breaking skills down into the micro skills needed to be successful, but there is certainly a danger that in doing this you actually remove all the challenge.

I like the idea of DoK levels as they are not about the content but the questions you ask. It is very easy to only ask DoK 1 questions which are essentially just repeating a process. And even DoK 2 questions only really have students applying the processes to new question types. To reach DoK 3 I need to consistently be building in the tasks I refer to in Swan's Top Tasks below.

But as a starting point, going through an exercise and rating each questions' DoK level will give me an idea of the level of challenge. Although DoK 1 and 2 are important at the very beginning of learning something, it is only through the DoK 3 tasks that students will get the chance to fully develop the concepts. So being aware of if I am including them will focus my attention on giving students enough challenge. 

When putting together future booklets I will actively look at the DoK level of the questions I include, and ensure there are some of all 3 levels.

Worked Examples
For the last year or so I have been embedding using example problem pairs in my teaching. I am at a point now where it is just how I teach, so I am looking to take them a little further.

The idea of using incorrect examples and examples that compare methods seems like a natural step. The incorrect examples from Algebra by Example look amazing, and I need to trawl through them to see what there is.

I still think it is important to first show students the correct method, but perhaps after an example problem pair, having an incorrect example prepared could be a way to have students discuss the method in more depth. I particularly like the prompts that come with the ones given by Algebra By Example, that are designed to get students thinking deeply about the errors.

I see this happening in one of two ways: a pre-prepared and printed example within the booklet; or I could work it 'live' on the board or through the visualiser.

I am not sure which is best, so will probably try each and see how it goes.

As far as comparing methods goes, I do try to build this in when students use multiple methods within the class (e.g. on quadratics...) but I could be more systematic about this. Again, planning them in advance and putting them within the booklets as ready to use discussion points could be a good way to move forward.

Concept/Non-Concept
Next year I will be teaching Year 7 for the first time in a while. Recently I have only been teaching IGCSE and IB level classes, and I am excited to have a non exam class. I am thinking I will try to make use of this strategy with this class. 

I have made limited use of Frayer Models before, but I want to make a bigger deal of looking at non-examples of concepts when first introducing them

The way I envisage this moving forward is as follows:

• Introduce the new concept (eg improper fractions) through an example
• Use a sequence of examples and non-examples to show the concept, including boundary examples
• Ask students to come up with a definition
• After hearing some definitions, give the formal definition
• 'Test' students on some further examples
• Have students fill in a Frayer Diagram with the definition and their own examples and non-examples

This kind of builds in the ideas from Engelmann and Carnine's work on Direct Instruction with the sequencing of the examples and non-examples, and I will be looking to follow the five principles they put forward (read more about this in this summary of The Components of Direct Instruction…).

Swan's Top Tasks
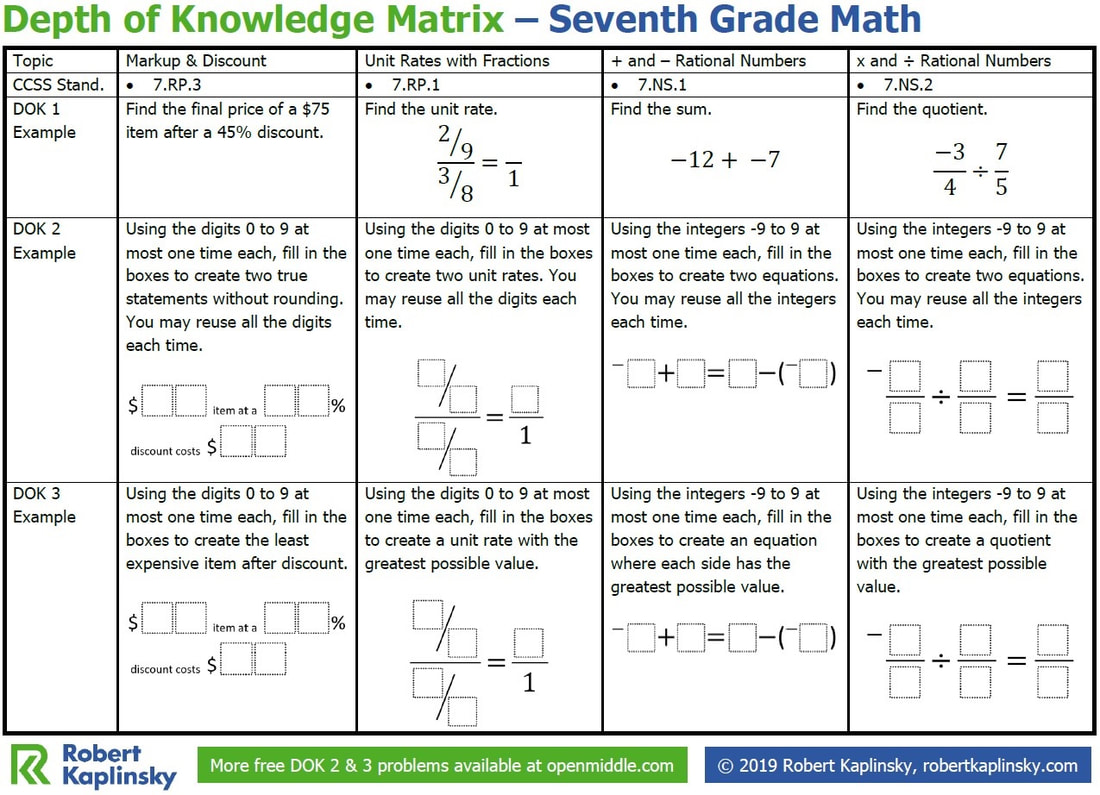
As part of the Standard's Unit, several task types were identified as being good practice activities for students to wrestle with mathematical ideas. Not sticking to just these tasks, I want to incorporate the following task types into my teaching more often.

https://www.openmiddle.com/create-a-system-of-two-equations/​

Open Middle style questions that have students place numbers in the boxes to create working questions, or to optimise results. These involve lots of practice, but also analysis of underlying connections and working systematically.

https://mathsvenns.com/solving-linear-equations-4/​

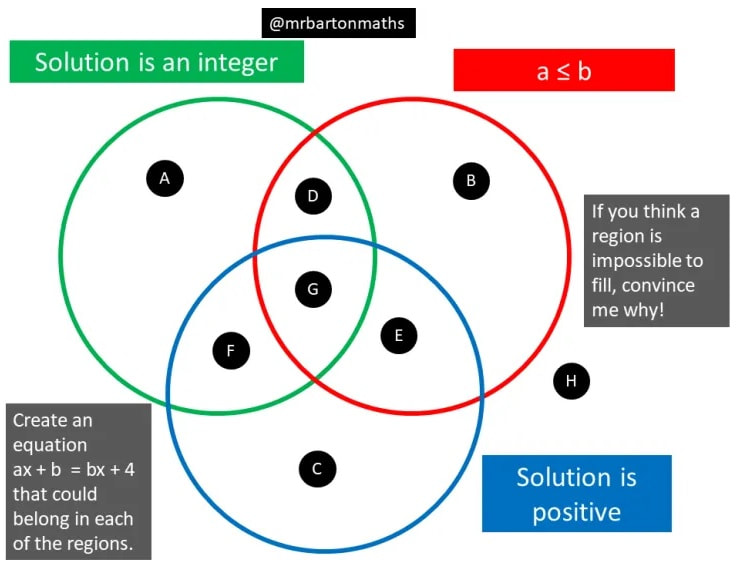
Maths Venns have students come up with mathematical objects to fit each of the regions of the diagram. These activities are accesible to all as you can just create an object and work out where it goes, but some strategic thinking is required to fill some of the regions.

https://www.openmiddle.com/logs/​

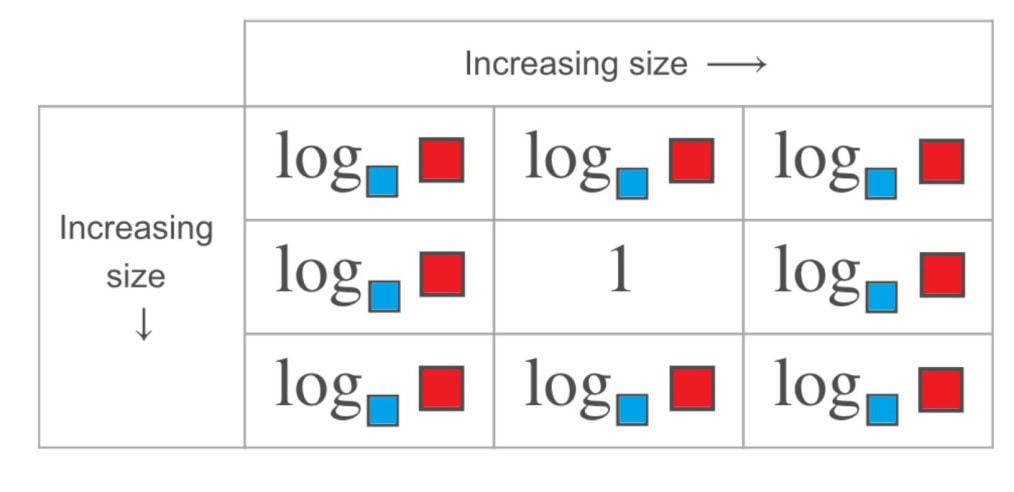
Two way increasing diagrams are great to work with two related ideas. Students have to fill in the eight remaining boxes with mathematical objects that follow the required rules of increasing or decreasing by both column and row. The one shown above comes from Open Middle and uses a similar structure to their other problems where students have to use the numbers 1-9 once each for red and once each for blue, but you can also leave the other boxes empty, and remove that restriction

These are all what Mr Barton would call "Purposeful Practice" as students not only get lots of practice with the mathematical ideas, but there is some systematic thinking or problem solving involved as well.

Plan the Questions
In much of my current planning I focus on my explanations, example problem pairs, and the questions students will answer in independent practice. What I have not thought much about before is planning questions to ask students as a whole class. Clearly this links to the ideas above, but I also went away and reread the excellent Thinkers from the ATM to get some inspiration for this target.

The first type of question is so simple, and yet so effective: Give me an example of… and another… and another. They also recommend simple changes to the questions along the lines of variation theory by asking "What if not?". So, for example, the question could be "Give me an example of a two numbers with a sum of 2…and another…and another." This could then be adjusted by thinking "What if not sum?" to get "Give me an example of a two numbers with a difference/product/quotient of 2…and another…and another." Or "What if not 2?" and we get "Give me an example of a two numbers with a sum of 2.13…and another…and another." Or even "What if not two numbers?" to give "Give me a definite integral with value 2…and another…and another."

There are then two adapted versions of this: Give an example, a peculiar example, a general example; and Give an easy and a hard example. 

These are such simple ideas to implement, but so powerful, but I know that I am not going to do it unless I start planning them deliberately before class

Whole Class Feedback and Codes
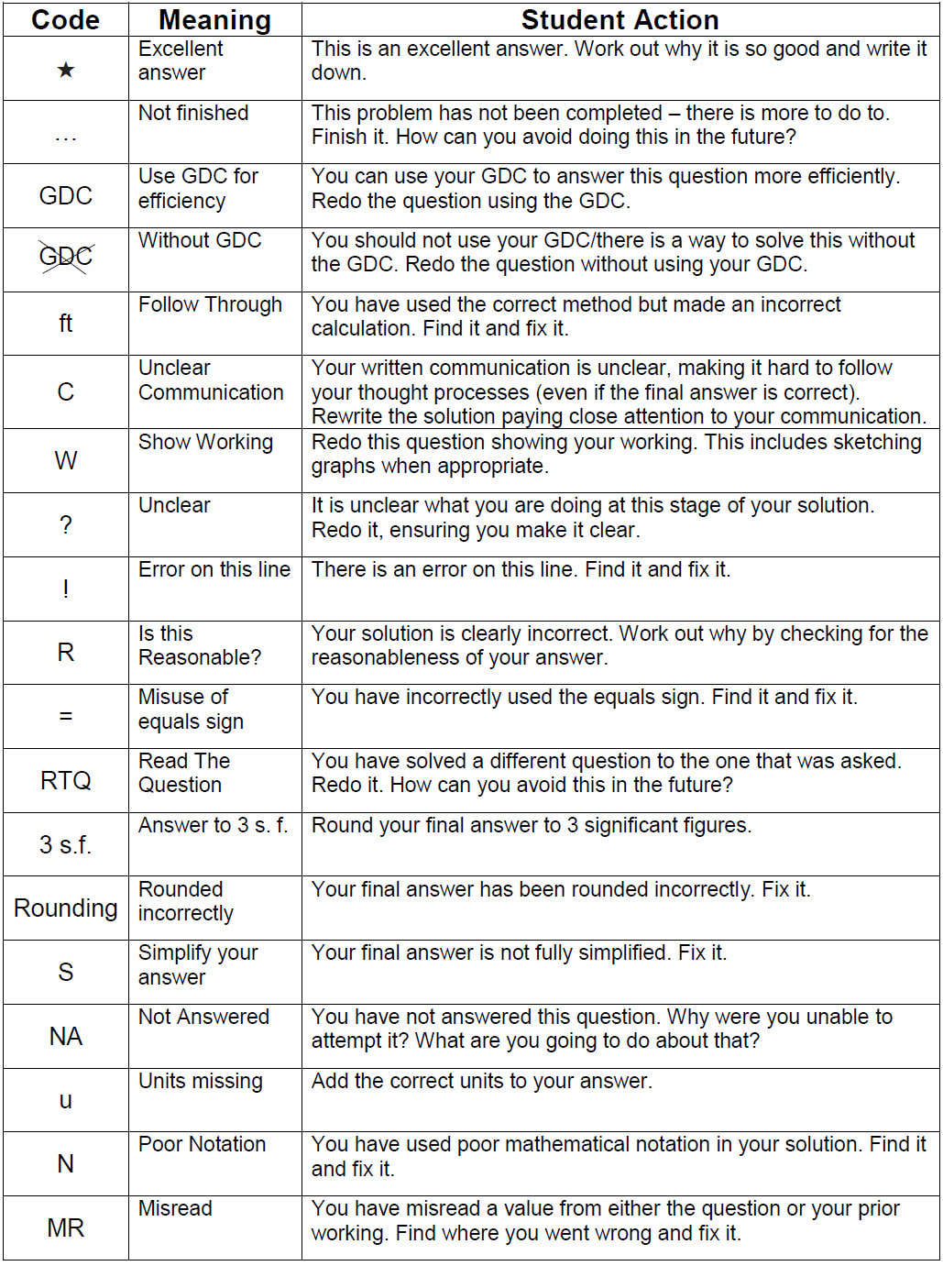
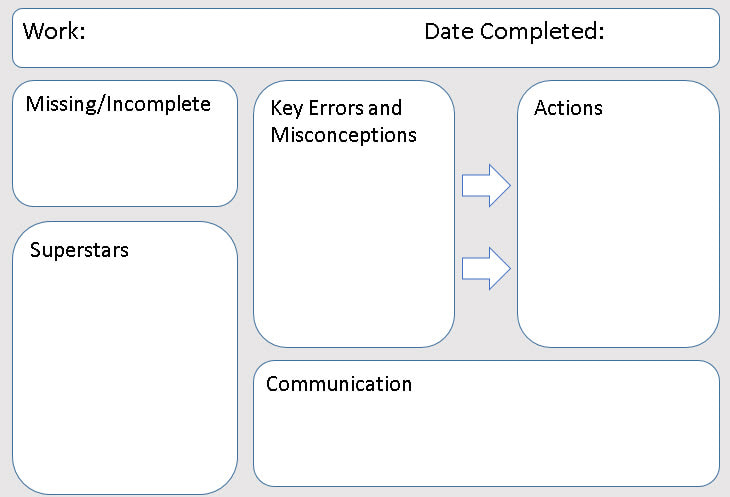
I have already started to implement this one in my teaching, which is actually two related ideas. When marking work I have always used some abbreviations for common mistakes (e.g. 3sf for "You should have rounded this answer to 3 significant figures"), but I have now put together an A5 sheet with a list of these codes that I use.

Giving one of these to each student allows them to look through their work and understand the problem. This also follows Dylan Wiliam's principle of the need for feedback to be more work for the recipient than the giver, as with each code there is also an associated action that the students need to follow.

Linked to this I have created a template of a Whole Class Feedback sheet (similar to those I have seen on twitter) where I can record points as I mark a class set of books, or quizzes. Similar to the codes, the most important part of  this template is the action box, which has been making me think about what I actually need to do for each of the issues that arise. Before this, I was much more ad-hoc about this, and would address those issues that needed it, usually by going through the question or a similar example. But now I think more carefully about the appropriate action to take (add it to a starter, reteach, have students teach each other, etc).

The Communication box is because that has been the agreed focus for my classes in terms of our Approaches to Learning Mathematics document, and this will change depending on the current focus

Concluding Remarks
With so many amazing ideas in this amazing book, there is bound to be something for every Maths teacher. But as McCrea herself says, it is best to focus on a couple of strategies and then embed them. So that is why I have chosen one from each section to work on over the next year.