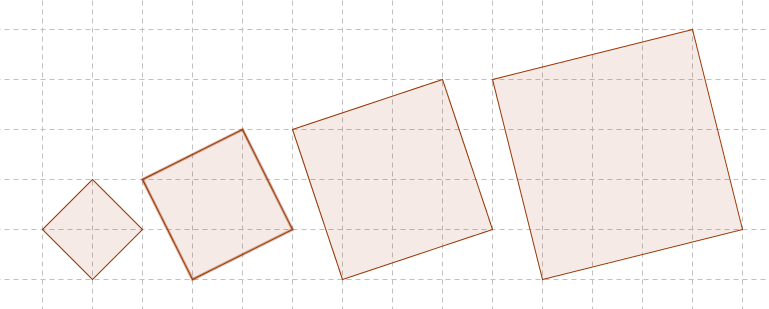
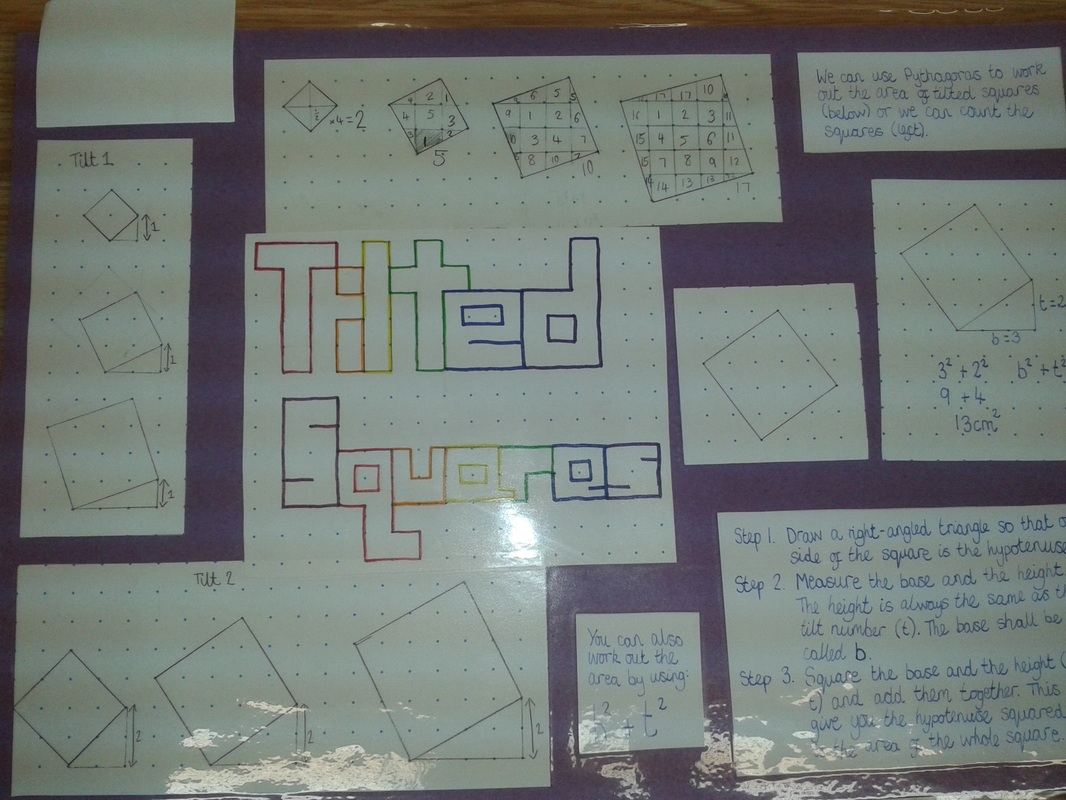
I had introduced my Year 7 students to Pythagoras' Theorem, and we had looked at using it tofind both the hypotenuse and shorter side, as well as using it to solve some worded questions. I was looking for something a little bit different to finish off the topic, and I remembered the Tilted Squares activity I made last year.
In the activity students have to investigate the area of squares that are slightly tilted, like the ones shown below.
I started the off by looking at this image, and discussing that these were squares of "tilt 1" and why we might say this. Then, without any advice, I gave them each some square dotted paper, and asked them to find the area of each of the squares with tilt one. I gave them 10 minutes to explore different ways to find the areas of each square, and most opted to split each square up and match pieces to make 1cm squares and count them up.
After 10 minutes, we came back as a class to discuss our methods, and any patterns we had spotted. A few had spotted the pattern in the areas, that they were increasing by the odd numbers each time (2, 5, 10, 17, ...), but then to my complete surprise and delight, one of them suggested what I was about to lead them on to. The girl said "well, there is a right angled triangle at the bottom, so obviously we use Pythagoras".
A few of the others in the class then made that ever so satisfying "ahhh" sound as it all clicked into place. There were still a few not quite sure what they meant, so I asked them to come to the front to demonstrate where the right angled triangle was, and what it was they meant.
Having done Perigal's Dissection a couple of lessons previously, she described perfectly how the area of the square was equal to the area of the squares on the two sides of the right angled triangle. The rest of the class had that realisation moment, and I hadn't even said anything about Pythagoras!
I then asked them to investigate "tilt 2" squares, and other tilts, but some of them immediately spotted the generalisation, and could tell me the area of any tilted square in a matter of seconds. I then had them start on their posters (which they were to finish for homework) on the Tilted Squares problem, saying they could either focus on "tilt 1" squares and how Pythagoras could be used there, or on other tilts, or even on the general method. I am looking forward to seeing the posters on Monday!
I am conviced that the reason they all grasped this so easily was the heavy emphasis that I put on the relationship between areas in Pythagoras' Theorem, as I have done the investigation before with Year 9, who use it in a very algebraic way, and they did not spot the relationship anywhere near as quickly or easily. And when they did get there, they went through the process of square rooting to find the length, to then square to find the are of the square, rather than neatly spotting that they already had the area, and didn't actually need to go through the process of square rooting.
A really enjoyable little investigation, that my class got a lot out of, and really demonstrated their very good understanding of what Pythagoras' Theorem is all about.
RSS Feed
