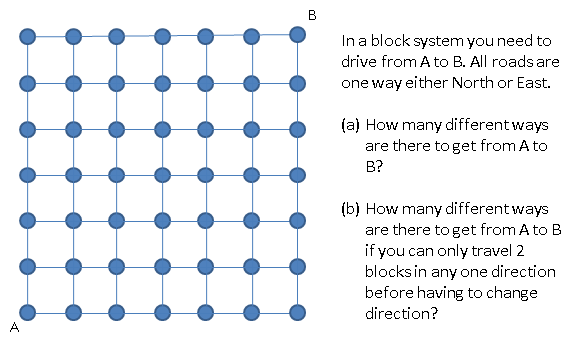
I am currently teaching the Cambridge Additional Maths course, parallel to the IGCSE course that we offer. As part of this I offer my students an extra after school session to come and practice questions from the Add Maths course, as we do not have much time in class to do the required practice. In this two hour session, I normally get between 2 and 10 students turn up, and they happily work through the questions, asking for help when needed. But this week one of the students came with a question she had seen on a Peruvian Maths Olympiad question, which I have turned into the image below.
The original 6x6 problem
Part (a) is something that I have seen several times before, and from my university days I remember it being an area of Maths called Taxicab Geometry. I am sure that it also popped up in the fantastic Dara O'Briain School of Hard Sums at some point as well.
For those that haven't seen it before, it is worth a look, and I warn you now, that if you want to solve the problems yourself, then stop reading now, as I am going to go through how I solved this problem...
Part (a) is a simple combinations problem. You have to travel 12 blocks in total, and you need 6 of them to be East. That is the total number of ways of travelling East is 12C6 = 924. It doesn't matter how you travel North, as this will be predetermined by your pathway East.
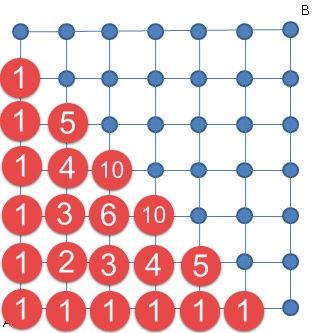
Another way to do this is to consider how many ways there are to get to closer points. There is only 1 way to reach any of the points due North or due East of A. Then the way to spot the pattern for inside points is that you must travel to that point via either the point to the West of it or to the South of it. And from each of these points there is only one way to get to the destination. So if there are 10 ways to get to the point to the West, and 5 ways to get to the point to the South, then there are 15 ways to get toour destination.
The number of ways to reach any point is the sum of the number of ways to reach the two points "before" it
This is just Pascal's Triangle (tilted a little bit), and is actually a very nice way to investigate the properties of this amazing sequence of numbers (though that is for another post).
I managed to answer this question for the student who asked quickly, and she was happy with the explanation (I did have to explain combinations to her, but since that comes up later in the course, that will be benificial anyway). The second part was another story...At first I thought maybe we could adjust the combinations method to find some way to cleverly divide out the routes we could not take because of the restriction...But this led nowhere. Then we tried to go via the triangle route, counting the number of paths available to closer points, and then extending this and trying to find a pattern...again, this go us nowhere as there seemed to be no pattern connecting the values. We got to that wonderful point where I said I was going to have to go away and look at the problem in more detail to try to come up with a solution. So that's what I did.
After staring at the problem for a while, I was still no closer to a solution, let alone an elegant one, so I turned to twitter for some inspiration. I got a response from @solvemymaths suggesting that it looked like a programming problem, so I decided to use a computer to help me find an answer
Knowing that every path must contain 12 blocks, I started by getting the computer to generate all possible binary numbers with 12 digits (made up of 0 for North and 1 for East). This was then simple to shorten to the 924 possible ways from A to B since we know there must be 6 Easts and 6 Norths, so the sum of the digits must be 6. So I removed all the options which did not have a digital sum of 6.
Now I had to remove all the options which contained either the string 111 or 000 which represent going three blocks in the same direction. Again, with a computer, this is fairly easy. After this process was complete, I got to the answer of 208 possible paths from A to B with this restriction.
After a bit of generalising, I came up with the widget below which will do the same process for different sized grids, and different block restrictions (code available here).
Grid Size = by
Max Blocks in one direction =
Max Blocks in one direction =
But being a mathematician, this still felt a bit like cheating, and I wanted to find a way to solve this problem without the use of the computer (though knowing the answer was certainly useful).
Trying to solve this manually the same way I used the computer was going to take forever, due to the huge number of possible options, so I had to come up with some other way. But the process of splitting it into binary options helped my thought processes. I ended up with the process shown in this document (first I solved the 4x4 version to check my method worked, before extending it to the 6x6 version).
My full solution to the 6x6 restricted taxicab problem.
I love it when students bring an interesting problem to class, as it shows they are interested, and also gives me a chance to discuss the wealth of Maths outside of the curriculum (something my students know too well, and are happy to exploit by distracting me and getting me to ramble on about some of the much more interesting areas of Maths). But this one was even better as it was one that I actually had to spend time working on to come up with a solution. The main reason I became a Maths teacher is because I love the subject, and I do not always get to DO maths as much as I like anymore, but this problem really made me remember why I love Maths, and why I teach it.
I would love to hear if anybody else comes up with a different way to solve this problem, so comment below...
RSS Feed
